Lösung von Aufg. 7.1 (WS 11/12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 16: Zeile 16:
 
   
 
   
 
Fall 2: Mathenerds 09:36, 26. Nov. 2011 (CET)
 
Fall 2: Mathenerds 09:36, 26. Nov. 2011 (CET)
 +
 +
 +
* Muss '''Fall 1''', d.h.  <math>\ E \cap g \ =  \ \lbrace  \rbrace</math>  überhaupt bewiesen werden?? Wenn E und g keinen Schnittpunkt haben, dann sind sie doch parallel...
 +
 +
* '''Fall 2''': <math>\ E \cap g \ =  \ \lbrace S\rbrace</math> <br /> ''Vor'':  Ebene E und eine nicht in ihr liegende Gerade g <br /> ''Beh'':<math>\ E \cap g \ =  \ \lbrace S\rbrace</math>  <br /> ''Ann'': <math>\ E \cap g \ =  \ \lbrace S,P\rbrace</math> <br /> Beweis: <br />
 +
{| class="wikitable"
 +
|-
 +
| Schritt || Begründung
 +
|- 
 +
| 1.) <math>\exists S,P\in g </math> || Axiom I/2, Vor.
 +
|-
 +
| 2.) g liegt in E|| Axiom I/5, Ann.,1.),Vor.
 +
|-
 +
 +
|}
 +
--> Widerspruch zur Vor., Annahme ist zu verwerfen --[[Benutzer:Wookie|Wookie]] 13:26, 28. Nov. 2011 (CET)
  
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Version vom 28. November 2011, 13:26 Uhr

Beweisen Sie: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.

Vor.: Ebene E und eine nicht in ihre liegende Gerade g Beh.: E geschnitten g kleiner gleich 1 Annahme: E geschnitten g größer 1

(1) E und nicht in ihr liegende Gerade g Vor (2) g: A,B,C koll Fall 1: E geschnitten g = {} Axiom 1/2, Def koll (3) es existiert P : P nicht Element g Axiom 1/2, Def koll (4) kompl (A,B,C,P) Def. kompl. (2), (3) (5) E2 (4) (6) E geschnitten E2 = {0} Axiom 1/10 (7) Widerspruch zur Anname

Fall 2: Mathenerds 09:36, 26. Nov. 2011 (CET)


  • Muss Fall 1, d.h. 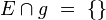\ E \cap g \ = \ \lbrace \rbrace überhaupt bewiesen werden?? Wenn E und g keinen Schnittpunkt haben, dann sind sie doch parallel...
  • Fall 2: \ E \cap g \ = \ \lbrace S\rbrace
    Vor: Ebene E und eine nicht in ihr liegende Gerade g
    Beh:\ E \cap g \ = \ \lbrace S\rbrace
    Ann: \ E \cap g \ = \ \lbrace S,P\rbrace
    Beweis:
Schritt Begründung
1.) 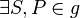\exists S,P\in g Axiom I/2, Vor.
2.) g liegt in E Axiom I/5, Ann.,1.),Vor.

--> Widerspruch zur Vor., Annahme ist zu verwerfen --Wookie 13:26, 28. Nov. 2011 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._7.1_(WS_11/12)&oldid=9799“