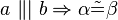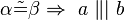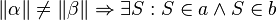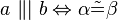Lösung von Aufgabe 2.2 S (SoSe 12)
Inhaltsverzeichnis |
Aufgabe 2.2
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt S geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel  und
und  . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
Lösungsvorschlag 1
a) Wenn zwei parallele Geraden a und b von einer dritten Geraden c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß.
b)
1.) Wenn a parallel zu b, so sind Alpha und Beta kongruent.(entspricht Stufenwinkelsatz)
2.) Wenn Alpha und Beta kongruent sind, so ist a zu b parallel .(entspricht nicht Stufenwinkelsatz)
3.) Wenn Alpha und Beta nicht kongruent sind, so exsistiert ein Punkt S, der Element von a und b ist.(entspricht Sws.)
- Hier muss man aufpassen, da die Abkürzung Sws für einen anderen Satz benutzt wird. --Tutor Andreas 15:09, 29. Apr. 2012 (CEST)
4.) Genau dann wenn a parallel zu b, sind alpha und beta kongruent.(entspricht nicht Stufenwinkelsatz)Zigzag
- Bitte setzt eure Signatur hinter eure Beiträge. Dazu müsst ihr in der Werkzeugleiste den Button "Deine Signatur mit Zeitstempel" auswählen. --Tutor Andreas 15:09, 29. Apr. 2012 (CEST)
Lösungsvorschlag 2
a) Stufenwinkelsatz: Stufenwinkel an geschnitten Parallelen sind kongruent zueinander.
b)
1.) Stufenwinkelsatz
2.) Umkehrung Stufenwinkelsatz
3.) a und b schneiden sich in einem Punkt S
4.) Stufenwinkelkriterium
--Funkdocta 15:09, 29. Apr. 2012 (CEST)
- Und welche Aussagen sind jetzt äquivalent zum Stufenwinkelsatz?--Tutor Andreas 15:13, 29. Apr. 2012 (CEST)
1) ist äquivalent, Stufenwinkelsatz
2) ist äquivalent, Umkehrung des Stufenwinkelsatz
3) nicht äquivalent
4) ist äquivalent, da Kriterium--Braindead 15:56, 2. Mai 2012 (CEST)
- Was bedeutet denn äquivalent? Vielleicht kann das jemand an dieser Stelle mit einer Wahrheitstabelle verdeutlichen.--Tutor Andreas 18:09, 2. Mai 2012 (CEST)
Zu 4.)
Ich versuchs mal mit der Wahrheitstabelle, zumindest das mit der mathematischen Schreibweise in der Tabelle hat nun geklappt. Ansonsten bin ich mir net so sicher, ob es so stimmt.
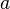
|
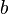
|
Fehler beim Parsen(Lexikalischer Fehler): \ a \ \|| \ b \ | 
|

|
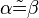
|
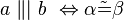
|
|---|---|---|---|---|---|---|
| w | w | w | w | w | w | w |
| f | w | f | f | w | f | w |
| w | f | f | w | f | f | w |
| f | f | w | f | f | w | w |
Anmerkung zur Aufgabenstellung bei 3
Es hat in der heutigen Übung etwas irritiert, dass erst S definiert wird als Schnittpunkte der Geraden a und c, sowie b und c. Später wird S dann nochmal in einen anderen Kontext gebracht. Unklar ist, dass beide S anscheinend lediglich Schnittpunkte sind und keinen Zusammenhang besitzen. --Mathen00b 12:44, 3. Mai 2012 (CEST)