Lösung von Zusatzaufgabe 4.4 S (SoSe 12)
1) Wenn vier Punkte nicht in der selben Ebene liegen, dann sind drei Punkte von ihnen auf der selben Ebene
2) 4 Punkte die nicht auf der selben Ebene sind, haben drei Punkte die nicht auf der selben Geraden liegen
3) Voraussetzung: nkomp (ABC)
Behauptung: nkoll (ABC)nkoll(BCD)
nkoll(CDA)
nkoll(BCA)
Annahme: nkomp (ABCD)koll (ABC) oBdA
1 Fall:
D  g
g
2 Fall: D ist nicht  g
g
Hallo hier mal ein direkter Beweis: Ist der so richtig?????
Vor: nkomp(A,B,C,D)
Beh: nkoll (A,B,C) oBdA
1:nnKomp(A,B,C,D) laut Vor
2:EX A,B,C,: nkoll(A,B,C) laut Ax I/3 (1) oBdA
3: nKoll(A,B,C) laut (2) q.e.d
--Nemo81 13:21, 28. Mai 2012 (CEST)
Hier mal indirekt:
Vor: nkomp(A,B,C,D)
Beh: nkoll(A,B,C)
Ann: koll(A,B,C), Fall 1: D nicht Element g, Fall 2: D Element g
Beweis:
Fall 1:
(1) koll(A,B,C); Ann
(2)  g: A,B,C
g: A,B,C  und D
und D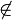 g; Ann, (1)
g; Ann, (1)
(3)  Ebene E: A,B,D
Ebene E: A,B,D  E; Ax. I/4, (2)
E; Ax. I/4, (2)
(4)  Ebene E: A,B,C,D
Ebene E: A,B,C,D  E; Ax. I/5, (2), (3)
E; Ax. I/5, (2), (3)
(5) komp(A,B,C,D); Def komp
Fall 2:
(1) koll(A,B,C); Ann
(2)  g: A,B,C
g: A,B,C  g und D
g und D g; Ann, (1)
g; Ann, (1)
(3)  g: A,B,C,D
g: A,B,C,D  g; (2)
g; (2)
(4)  Ebene E: A,B,C,D
Ebene E: A,B,C,D  E; Ax. I/5, (3)
E; Ax. I/5, (3)
(5) komp(A,B,C,D)
--Mohnkuh 22:31, 30. Mai 2012 (CEST)

