Lösung von Zusatzaufgabe 4.4 S (SoSe 12)
1) Wenn vier Punkte nicht in der selben Ebene liegen, dann sind drei Punkte von ihnen auf der selben Ebene
2) 4 Punkte die nicht auf der selben Ebene sind, haben drei Punkte die nicht auf der selben Geraden liegen
3) Voraussetzung: nkomp (ABC)
Behauptung: nkoll (ABC)nkoll(BCD)
nkoll(CDA)
nkoll(BCA)
Annahme: nkomp (ABCD)koll (ABC) oBdA
1 Fall:
D  g
g
2 Fall: D ist nicht  g
g
Hallo hier mal ein direkter Beweis: Ist der so richtig?????
Vor: nkomp(A,B,C,D)
Beh: nkoll (A,B,C) oBdA
1:nKomp(A,B,C,D) laut Vor
2:EX A,B,C,: nkoll(A,B,C) laut Ax I/3 (1) oBdA
3: nKoll(A,B,C) laut (2) q.e.d
--Nemo81 13:21, 28. Mai 2012 (CEST)
- Diesen Beweis halte ich für nicht richtig. In Schritt 2 wird ja direkt gesagt, dass A,B,C nicht auf einer Geraden liegen... aber was ist mit dem Punkt D. Gibt es dann eine Gerade die z.B. A,B,D enthält? --Tutor Andreas 11:23, 12. Jul. 2012 (CEST)
Hier mal indirekt:
Vor: nkomp(A,B,C,D)
Beh: nkoll(A,B,C)
Ann: koll(A,B,C), Fall 1: D nicht Element g, Fall 2: D Element g
Beweis:
Fall 1:
(1) koll(A,B,C); Ann
(2)  g: A,B,C
g: A,B,C  g und D
g und D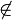 g; Ann, (1)
g; Ann, (1)
(3)  Ebene E: A,B,D
Ebene E: A,B,D  E; Ax. I/4, (2)
E; Ax. I/4, (2)
(4)  Ebene E: A,B,C,D
Ebene E: A,B,C,D  E; Ax. I/5, (2), (3)
E; Ax. I/5, (2), (3)
(5) komp(A,B,C,D); Def komp
Fall 2:
(1) koll(A,B,C); Ann
(2)  g: A,B,C
g: A,B,C  g und D
g und D g; Ann, (1)
g; Ann, (1)
(3)  g: A,B,C,D
g: A,B,C,D  g; (2)
g; (2)
(4)  P: nkoll(A,B,P); Ax I/3
P: nkoll(A,B,P); Ax I/3
(5)  Ebene E: A,B,C,D,P
Ebene E: A,B,C,D,P  Ebene E; Ax. I/4, Ax. I/5, (4), (3)
Ebene E; Ax. I/4, Ax. I/5, (4), (3)
(6) komp(A,B,C,D)
--Mohnkuh 22:31, 30. Mai 2012 (CEST)
- Von der Idee her passt es. Ich konnte es auch nachvollziehen, aber ich finde es immer gut, wenn man lieber ein paar Schritte mehr macht, dann kann man es besser nachvollziehen. In den einzelnen Schritten bzw. Begründungen steckt teilweise sehr viel drin.--Tutor Andreas 11:27, 12. Jul. 2012 (CEST)
Lösungsversuch Nummero6/Tchu Tcha Tcha:
1.) Wenn vier Punkte nicht in ein und derselben Ebene liegen, dann liegen auch jeweils drei Punkte von ihnen nicht auf ein und derselben Geraden.
2.) Von vier Punkten die nicht in ein und derselben Ebene liegen, liegen auch jeweils drei Punkte von ihnen nicht auf ein und derselben Geraden.
3.) folgt..
--Tchu Tcha Tcha 10:48, 8. Jun. 2012 (CEST)

