Lösung von Aufgabe 4.4 S (SoSe 12)

Aufgabe 4.4

Die Aufgabe

Beweisen Sie Satz I.6: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.

Lösung von Nemo81

Vor: Ebene E und nicht in ihr liegende Gerade g
Beh: E geschnitten g höchstens einen Punkt gemeinsam

Beweis durch Widerspruch
Ann: E geschnitten g mindestens zwei Punkte gemeinsam
Beweise:

Beweisschritt	Begründung
1) Ebene E und nicht in ihr liegende Geradeng.	Vor
2) E geschnitten g = Punkt P und es existiert mindestens ein Punkt Q für den gilt Q ist nicht Element der Ebene.	(Beh)
3) Punkte PQ liegen in der Ebene E.	( Ann)
4) PQ bildet Gerade g die in der Ebene E liegt.	(3), Axiom I/1, Axiom I/5)
5)Widerspruch zur Vor.	(4),3),2))

--Nemo81 15:10, 20. Mai 2012 (CEST)

Hinweis von Tutor Andreas

• Die Idee ist soweit ganz gut. Mich verwirrt nur, dass die Behauptung im Beweis vorkommt und dass sich Schritt 2 und Schritt 3 widersprechen. Dies sollte noch verbessert werden.--Tutor Andreas 18:27, 22. Mai 2012 (CEST)

Frage von unserer Mutter

Sollte man nicht 2 Fälle betrachten?

Fall_1: Wie oben. Gemeinsamer Punkt.

Fall_2: Parallelität. Keine Punkte gemeinsam. Siehe Aufgabenstellung : "Beweisen Sie Satz I.6: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam." Ein oder kein Punkt gemeinsam? „deine Mutter 13:01, 7. Jun. 2012 (CEST)“

Kommentare M.G.

@ deine Mutter

Wir gehen also von einer Geraden $g$ und einer Ebene $E$ aus. Diese mögen derart zueinander liegen, dass die Gerade $g$ nicht vollständig in der Ebene $E$ liegt.

Zeigen sollen wir jetzt, dass $g$ und $E$ maximal einen Punkt gemeinsam haben können.

Unsere Arbeit wäre getan, wenn wir gezeigt hätten, dass $g$ und $E$ nicht mehr als einen Punkt gemeinsam haben können. Diese erledigen wir sinnvollerweise indirekt per Widerspruch. Wenn uns das gelungen ist, haben wir gezeigt, dass $g$ und $E$ nicht mehr als einen Punkt gemeinsam haben können.

Es wären jetzt natürlich zwei Fälle möglich:

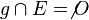1. $g \cap E = \not O$g
2. $\exist P: P \in g \wedge P \in E$

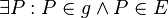
Die fleißige Studentin / der fleißige Student mag sich jetzt gern damit auseinandersetzen, ob beide Fälle wirklich auftreten können. Sie/er muss es aber nicht, denn wir sollten ja nur zeigen, dass die beiden Punktmengen nicht mehr als einen Punkt gemeinsam haben können. Ob es ggf. vielleicht auch gar kein Punkt sein könnte, war nicht gefragt. Oder?--*m.g.* 13:42, 7. Jun. 2012 (CEST)

zum Beweis

Der Beweis von Nemo81 enthält einen schwerwiegenden Fehler, der den gesamten Beweis letztlich zunichte macht:

Vorsicht: Ein Beweisschritt wird mit der Behauptung begründet.

Wenn so etwas logisch korrekt wäre, dann könnte man doch jeden Beweis letztlich auf die folgende Art und Weise führen:

Voraussetzung: Aussage V Behauptung: Aussage B

Nr.	Beweisschritt	Begründung
(1)	Aussage B gilt	nach Behauptung