Vektorräume 2012 13

Definition des Begriff des Vektorraums

Eine nicht leere Menge V zusammen mit einer inneren Verknüpfung

$+: V \times V \to V$, $(v,v)\mapsto v+v$

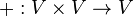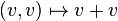
und der äußeren Verknüpfung

${\cdot}: \mathbb{R} \times V \to V$, $(\lambda ,v)\mapsto \lambda \cdot v$

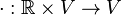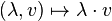
heißt reeler Verktorraum, falls folgende Bedingungen erfüllt sind:

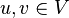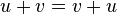A1: Für beliebige $u,v \in V$ gilt $u+v=v+u$ (Kommuntativität der Addition).

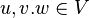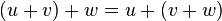A2: Für beliebige $u,v.w \in V$ gilt $(u+v)+w=u+(v+w)$. (Assoziativität der Addition)

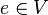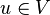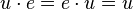A3: Es gibt ein neutrales Element $e\in V$, mit dem für alle Elemente $u\in V$ gilt: $u\cdot e = e\cdot u = u$. (Existenz eines neutralen Elements/Nullvektor)

A4: Zu jeden 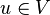$u\in V$ existiert ein Gegenvektor 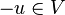$-u \in V$ mit$u+(-u)=e$

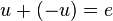
S1: Für beliebige 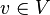$v \in V$ gilt $1\cdot u =u$.

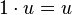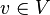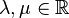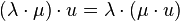S2: Für beliebige $v \in V$ und beliebige $\lambda, \mu \in \mathbb{R}$ gilt: $(\lambda \cdot \mu)\cdot u= \lambda\cdot(\mu\cdot u)$ (Assoziativität der Multiplikation von Vektoren mit reelen Zahlen)

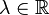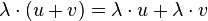S3: Für beliebige math>u,v \in V</math> und beliebige $\lambda \in \mathbb{R}$ gilt: $\lambda \cdot (u+v)=\lambda \cdot u +\lambda \cdot v$ (1.Distributivgesetz)

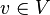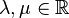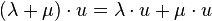S4: Für beliebige $v \in V$ und beliebige $\lambda, \mu \in \mathbb{R}$ gilt: $(\lambda + \mu)\cdot u=\lambda \cdot u + \mu \cdot u$ (2.Distributivgesetz)

Bemerkung:

Die Eigenschaften A1-A4 lassen sich zusammenfassen, dass 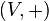$(V, +)$ eine Abelsche Gruppe bildet.

(Quelle: Filler: Elementare Lineare Algebra. Spektrum Akademischer Verlag)