Lösung von Zusatzaufgabe 9.1P (SoSe 13)
- Was versteht man unter der Parallelentreue einer Geradenspiegelung?
- Beweisen Sie die Parallelentreue einer Geradenspiegelung.
Tipp: Im Wiki nachlesen und den Beweis dann indirekt führen.--Tutorin Anne 18:21, 26. Jun. 2013 (CEST)
Inhaltsverzeichnis |
Beweis von Blumenkind
- Zwei Geraden sind parallentreu, wenn bei der Geradenspiegelung zueinander parallelen Geraden p1 und p2 ebensfalls zueinader parallel abgebilder werden. Kurz formuliert:
--> p1 II p2 --> p1` II p2 ` wobei Sg (P1)= P1` und Sg(P2)=P2`
- Beweisdurchführung
- Vor.: p1 II p2, Sg (P1)= P1` und Sg(P2)=P2`
- Beh.: p1`II p2`
1. Sg (p1)= p1` und Sg(p2`) Voraussetzung
2. p1 II p2 Voraussetzung
3.
--> HILFE!!!! ICH KOMM NICHT MEHR WEITER. IRGENDWIE BIN ICH DURCHEINANDER GEKOMMEN. WAS MACHE ICH FALSCH?--Blumenkind 18:51, 4. Jul. 2013 (CEST)BLUMENKIND 18:50, 4.Juli
Probier es mal, wie Anne schon oben angemerkt hat, über einen indirekten Beweis. Wie muss also die Annahme lauten?--TobiWan 12:28, 5. Jul. 2013 (CEST)
- Voraussetzung und Behauptung sind richtig.
- Das ist leider kein Beweis, da nur, weil Geraden auf Geraden abgebildet werden, diese nicht unbedingt parallel sind.
- Tipp: Gehe indirekt vor, indem du annimmst dass P1 und p2 einen Schnittpunkt haben.--Tutorin Anne 14:22, 8. Jul. 2013 (CEST)
Beweis von Regenschirm
| Voraussetzung | 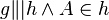
|
| Behauptung | 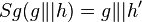
|
| Annahme | 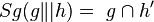
|
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | 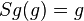 |
Voraussetzung, |
| 2 | 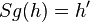 |
Voraussetzung, |
| 3 | 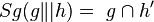 |
Annahme |
| 4 | 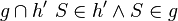 |
1) 2) 3) |
| 5 | 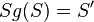 |
4) Def. Geradenspiegelung |
| 6 | 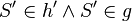 |
2) 5) |
| 7 | 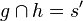 |
6) |
| 8 | Widerspruch, Annahme ist zu verwerfen, Behauptung stimmt | 7) |
--Regenschirm 22:30, 11. Jul. 2013 (CEST)
Die Beweisidee ist absolut richtig, so wie auch die Abfolge der Schritte und die meisten Begründungen (manche sind nicht komplett). Die formale Schreibweise ist aber ziemlich verdreht und so nicht richtig. Zudem scheinen mir manchmal ' zu fehlen.--Tutorin Anne 16:47, 12. Jul. 2013 (CEST)
-
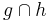 kann als "schneidet" gelesen werden. Das ist trotzdem eine Mengenoperation "Schnittmenge von g und h" und kann deshalb auch eine leere Menge sein. Deshalb bitte immer dazu schreiben, ob der Schnitt leer ist oder eben nicht.
kann als "schneidet" gelesen werden. Das ist trotzdem eine Mengenoperation "Schnittmenge von g und h" und kann deshalb auch eine leere Menge sein. Deshalb bitte immer dazu schreiben, ob der Schnitt leer ist oder eben nicht.
- Tendenziell nutzen ganz viele die Definition von Geradenspiegelung (und anderen Spiegelungen) für so ziemlich alles. Da steht aber fast nichts drin! Was überhaupt?
Ich schreibe den Beweis hier nochmal. Die Schritte sind noch zu begründen: --Tutorin Anne 16:47, 12. Jul. 2013 (CEST)
Beweisschritte zu Ergänzen
| Voraussetzung | a II b, 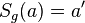 und und 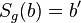
|
| Behauptung | a' II b' |
| Annahme | a' |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | 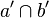 = {S'} = {S'} |
Annahme |
| 2 | 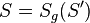 |
1) Def. Geradenspiegelung |
| 3 | 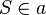 und und 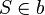 |
1) 2) |
| 4 | 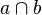 = {S} = {S} |
3) |
| 5 | |
4) |
| 6 | Widerspruch zur Voraussetzung | 5) Voraussetzung |
Müsste bei Schritt 5) nicht a II b stehen?--Regenschirm 19:00, 14. Jul. 2013 (CEST)
- Denke Regenschirm, so ist es! Danke auch fürs Ergänzen.
- Die Begründungen für Schritt 3, 4 und 5 sollten noch zusätzlich durch Definitionen oder Eigenschaften ergänzt werden.--Tutorin Anne 10:00, 15. Jul. 2013 (CEST)
Beweis von Nolessonlearnd
Voraussetzung: 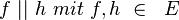
--Nolessonlearned 20:43, 15. Jul. 2013 (CEST)
Behauptung: 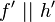
--Nolessonlearned 20:43, 15. Jul. 2013 (CEST)
Annahme: 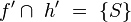
--Nolessonlearned 20:43, 15. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 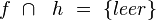
|
Voraussetzung |
| 2) | 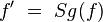
|
Eigenschaft von Sg |
| 3) | 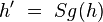
|
Eigenschaft von Sg |
| 4) | 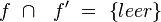
|
(2); Geradentreue von Sg |
| 5) | 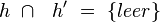
|
(3); Geradentreue von Sg |
| 6) | 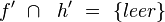
|
(4); (5);
Widerspruch zur Annahme. Annahme ist zu verwerfen. Behauptung stimmt. q.e.d. |

