14)
Aus Geometrie-Wiki
Version vom 5. Februar 2014, 10:10 Uhr von Tutorin Anne (Diskussion | Beiträge)
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Beweis: Geg. sind zwei konvexe Punktmengen  und
und 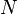 mit
mit 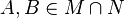
zu zeigen: 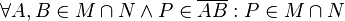
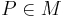 , weil
, weil 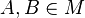 und
und  ist konvex.
ist konvex.
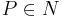 , weil
, weil 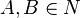 und
und 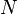 ist konvex.
ist konvex.
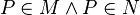
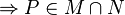
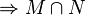 ist konvex.
ist konvex.
--EarlHickey (Diskussion) 12:09, 4. Feb. 2014 (CET)
Der Beweis ist von den Schritten korrekt, allerdings teilweise recht ungenau und nicht komplett begründet.
Du hast z.B. nicht begründet, warum 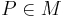 ist. In der Voraussetzung steht ja nur
ist. In der Voraussetzung steht ja nur 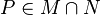 Dafür gibt es eine Definition. Welche?
Dafür gibt es eine Definition. Welche?
Das selbe gilt für deine zwei letzten Schritte, der zwar richtig sind, aber nicht begründet sind. --Tutorin Anne (Diskussion) 10:10, 5. Feb. 2014 (CET)

