Übung Aufgaben 10 (SoSe 22)

Aufgabe 10.1

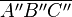Das Dreieck $\overline{ABC}$ wurde durch die Nacheinanderausführung zweier verschiedener Geradenspiegelungen auf das Dreieck $\overline{A''B''C''}$ abgebildet. Konstruieren Sie die beiden Spiegelgeraden.

Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren

Lösung von Aufgabe 10.1P (SoSe_22)

Aufgabe 10.2

Beweisen Sie Satz IX.2:
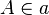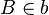Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten $A\in a$ und $B\in b$, die von S jeweils verschieden sind. Wir betrachten die Verkettung $S_{a}\circ S_{b}$. Für einen beliebigen Punkt P und seinen Bildpunkt $P''=S_{a}\circ S_{b}(P)$ gilt: $\left| \angle PSP'' \right| =2\cdot\left| \angle ASB \right|$.
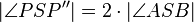Lösung von Aufgabe 10.2P (SoSe_22)

Aufgabe 10.3

Das Rechteck $\overline{ABCD}$ soll durch eine Drehung auf das blaue Rechteck abgebildet werden. Konstruieren Sie den Drehpunkt. Wo müssen die beiden Achsen liegen, wenn die Drehung durch eine Verkettung zweier Achsenspiegelungen erzeugt werden soll?
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.

Lösung von Aufgabe 10.3P (SoSe_22) 1. Schritt: Verbindung der Punkte A und A`zur Strecke AA`, Verbindung der Punkte B und B`zur Strecke BB` 2. Schritt: Konstruktion der Mittelsenktrechten von der Strecken AA` zu a und BB` zu b 3. Schritt: Die Mittelsenkrechten a und b schneiden sich im Punkt S, welcher der Drehpunkt ist--Kwd077 (Diskussion) 13:34, 27. Jun. 2022 (CEST)

Aufgabe 10.4

Beweisen Sie: Bei Spiegelungen, Stöße beim Billard über Bande, etc. gilt stets: Einfallswinkel $\alpha$ gleich Ausfallswinkel $\beta$ (siehe GeoGebra-Applet).

Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren

Lösung von Aufgabe 10.4P (SoSe_22)

Aufgabe 10.5

Beweisen Sie Satz IX.3: Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 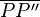$\overline{PP''}$, mit $P''=S_a\circ S_b(P)$.
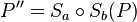Lösung von Aufgabe 10.5P (SoSe_22)