Lösung von Aufgabe 10.5P (SoSe 22)

Beweisen Sie Satz IX.3: Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 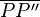$\overline{PP''}$, mit $P''=S_a\circ S_b(P)$.
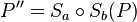Vor: Punktspiegelung an Sa, Sb, Sa schneidet Sb in S, P``= Sa verkettet mit Sb(P), a steht senkrecht auf b Beh: S ist Mittelpunkt von der Strecke PP``

Beweis: 1. a steht senkrecht auf b, a schneidet b in S, begründung: Vor 2. P ist genau dann Element von a, wenn man a senkrecht b um S soweit dreht, bis P au a zu liegen kommt, Begründung: 1., Vor, Eigenschaft Punktspiegelung, Def. Drehung 3. P`=Sa(P)=P, Begründung: 1., 2., Def. Geradenspiegelung 4. P``= Sb(P`), Begründung: 3., Def Fixgerade, da a Fixgerade zu Sb ist 5. Abstand PS = Abstan SP``, Begründung: 4., def Geradenspiegelung, Streckentreue 6. S ist Element von der Strecke PP``, Begründung:2.,3.,4., 5.,Def Drehung, Def Mittelpunkt--Kwd077 (Diskussion) 16:14, 27. Jun. 2022 (CEST)

guter Beweis c:--Matze2000 (Diskussion) 10:49, 6. Jul. 2022 (CEST)