Lösung von Aufg. 13.6 (SoSe 11)

Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz

In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.

Also Voraussetzung: Wir haben ein Dreieck.
Behauptung: Mindestens zwei Innenwinkel sind spitze Winkel, also ihr Maß ist geringer als 90.
Annahme für Widerspruch: Nein, es gibt auch Dreiecke, in denen zwei Innenwinkel nicht-spitze Winkel sind, also jeweils das Maß 90 oder mehr (bis zu 180) haben.
I. An einem der beiden stumpfen Innenwinkel, nennen wir ihn Alpha, liegt ein Außenwinkel an, den wir ab jetzt Alpha-Strich nennen (Begründung: Definition Außenwinkel)
II. Dieser Außenwinkel Alpha-Strich muss ein stumpfer Winkel sein. (Begründung: Schwacher Außenwinkelsatz und Annahme, nach der neben Alpha ja noch ein Innenwinkel nicht-spitz ist).
III. Alpha und Alpha-Strich sind supplementär, da sie Nebenwinkel sind (Begründung: Definition Außenwinkel, Definition Nebenwinkel und Supplementaxiom)
IV. Die Größe des Gesamtwinkels, der aus der Addition von Alpha und Alpha-Strich resultiert, ist größer als 180. (Begründung: Rechnen in R, Definition stumpfe Winkel)
V. Das ist ein Widerspruch zu III (Begründung: Definition supplementär = Summe 180). Es kann also (in unserer Geometrie) keine Dreiecke geben, die zwei nicht-spitze Innenwinkel haben.

Genügt das so? --WikiNutzer 12:16, 13. Jul. 2011 (CEST)
Dieser Beweis klingt logisch. Ich mache noch eine Skizze dazu, dann ist es leichter nachvollziehbar.--Tutor Andreas 18:13, 13. Jul. 2011 (CEST)

So müsste auch gehen, ist ähnlich aber einfacher.

Vor: Dreieck ABC mit schulüblichen Bez.
Beh: mindestens zwei Winkel sind kleiner 90

Beweis per Widerspruch:
Annahme: Zwei Winkel sind nicht kleiner 90.
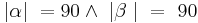
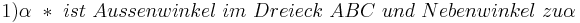z.z. oBdA: $| \alpha | \ = 90 \wedge \ | \beta \ | \ = \ 90$

$\ 1) \alpha \ * \ ist \ Aussenwinkel \ im \ Dreieck \ ABC \ und \ Nebenwinkel \ zu \alpha$ (Def. Außenwinkel, Def. Nebenwinkel)
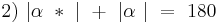$\ 2) \ | \alpha \ * \ | \ + \ | \alpha \ | \ = \ 180$ (1, Supplementax)
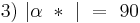$\ 3) \ | \alpha \ * \ | \ = \ 90$ (2, Rechnen in R)
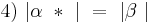$\ 4) \ | \alpha \ * \ | \ = \ | \beta \ |$ (Annahme, 3)
Hier kommt es zum Widerspruch zum schwachen Außenwinkelsatz, nach dem 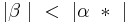$\ | \beta \ | \ < \ | \alpha \ * \ |$ gelten müsste.

Die Annahme ist also zu verwerfen, es gilt die Behauptung. ---phil- 14:05, 17. Jul. 2011 (CEST)