12)
Entwerfen Sie eigene Klausuraufgaben für Ihre Kommilitoninnen und Kommilitonen und stellen Sie diese hier ein. Schreiben Sie bitte keine Übungs- oder Tutorienaufgaben ab, sondern erfinden Sie wirklich neue eigene Aufgaben. Ordnen Sie Ihre Aufgaben in Schwierigkeitsgrade ein.
- Leichte Aufgaben:
Definiere Wechselwinkel
Es seien a, b zwei nicht identische Geraden, wenn a und b von einer weiteren Geraden c (die nicht identisch zu a und b) geschnitten werden, dann sind Wechselwinkel die Winkel, welche bezüglich c in verschiedenen Halbebenen liegen und bezüglich a in der gleichen Halbebene liegen und bezüglich b in der gleichen Halbebene liegen.
Meint ihr, diese Definition ist korrekt?--Miriam 10:13, 6. Jan. 2012 (CET)
- Die zwei sind dann Wechselwinkel.--RicRic 07:39, 10. Jan. 2012 (CET)
Ich habe versucht, deine Definition darzustellen.
Allerdings stimmt das noch nicht ganz. Denn die Winkel liegen nicht komplett innerhalb der selben Halbebene bezüglich a und b.
Deine Definition ist also noch nicht ganz korrekt.
--Tutorin Anne 22:52, 10. Jan. 2012 (CET)
Definiere Achtelkreis:--RicRic 07:39, 10. Jan. 2012 (CET)
...
- Mittelschwere Aufgaben:
1. Definiere ein Quadrat, beziehe dich dabei auf Strecken!
- Ein Quadrat ist ein Viereck bei dem drei Strecken konguent sind und zwei Seiten senkrecht aufeinander stehen.--RicRic 07:39, 10. Jan. 2012 (CET)
1.b. Definiere das Innere des Quadrates!
--RicRic 21:20, 21. Dez. 2011 (CET)
- Es sei ABCD ein Quadrat, das innere des Quadrates ist die Schnittmenge von AB,C+ mit BC,D+ mit CD,A+ mit DA,B+.
- Gehören die Seiten beim Quadrat zum inneren dazu? Bei der Halbebene, bei den Winkel nehmen wir sie dazu, ist sicherlich beides möglich, aber was ist Sinnvoll?--RicRic 07:39, 10. Jan. 2012 (CET)
...
Aus einer alten Probeklausur, wir haben leider die Lösung nicht und sin uneinig, bitte fleißig mit abstimmen! gRh sei definiert als: Die Geraden g und h haben genau einen Punkt gemeinsam. Welche Aussagen treffen zu? 1. R ist keine Relation in der Menge aller Geraden. 2. R ist eine reflexive Relation in der Menge aller Geraden. 3. R ist eine symmetrische Relation in der Menge aller Geraden. 4. R ist eine transitive Relation in der Menge aller Geraden.
--RicRic 10:13, 28. Dez. 2011 (CET)
- Schwere Aufgaben:
Beweisen Sie den folgenden Satz: Wenn Alpha ein rechter Peripheriewinkel über der Sehneeines Kreises k ist, dann ist
ein Durchmesser des Kreises k.--Schambes 19:56, 28. Dez. 2011 (CET)
Dies ist eine Aufgabe aus der letzten ATP. Wir waren gersten in der Lerngruppe sehr gefrustet, da wir mit der Lösung nichts anfangen konnten, wir haben lange mit dem Aplet von Tutorim 3 experimentiert, und sind der Meinung, es müsste heißen:
Zu meiner Begründung, der erste Teil, wenn die Kreise nicht ineinander liegen, und die Summe der zwei Radien kleiner ist als der Abstand der beiden Mittelpunkte, so haben die Kreise keinen Schnittpunkt und sehen somit nicht in Relation. Das Gleich zeichen würde ich auch weg lassen, da es heißt gemeinsame Punkte und nicht einen gemeinsamen Punkt somit also mindestens zwei. Den hintern Teil mit der Differenz der Radien kann ich nachvollziehen, wenn die Kreise ineinander liegen. Würde aber das gleich weg lasen. Wie seht Ihr das?--RicRic 14:10, 3. Jan. 2012 (CET) Ja genau ist in der Lösung unserer Meinung nach eindeutig Falsch!!! Möchten nicht wissen wie viele arme Komilitonen dewegen unberechtigt durchgefallen sind.--LGDo12 15:48, 5. Jan. 2012 (CET)
RicRic, Sie haben natürlich recht, dass hier in der angegebenen Lösung das erste 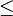 -Zeichen ein
-Zeichen ein 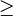 -Zeichen sein muss. Bitte seien Sie deswegen nicht frustiert, sondern erfreut, dass Sie diesen Fehler gefunden haben, super.
-Zeichen sein muss. Bitte seien Sie deswegen nicht frustiert, sondern erfreut, dass Sie diesen Fehler gefunden haben, super.
LGDo12, Sie können aber sicher sein, dass deswegen niemand unberechtigt durchgefallen ist. Die Vorstellung, dass wir Klausuren korrigieren (können), indem wir eine Musterlösung an die Seite legen und blind diese abarbeiten ist völlig falsch. Vielmehr sind wir auch aufgrund der vielfältigen Lösungsvorschläge in den Klausuren gezwungen, jede Klausur und jede Lösung individuell durchzuarbeiten. Bei Durchfallern dann sogar mehrmals. Die richtige Lösung der Aufgabe finden Sie übrigens auch in den Lösungen von Tutorium 3.
RicRic, Ich bin übrigens der Meinung, dass die Aussage: gemeinsame Punkte zu haben, auch auf genau einen gemeinsamen Punkt zutrifft, sonst müsste es nämlich heißen: mind. zwei gemeinsame Punkte. Aber auch darüber kann man sicherlich trefflich diskutieren! In der Klausur haben wir beide Lösungen akzeptiert!--Schnirch 21:26, 7. Jan. 2012 (CET)
...
Beweise!
Genau dann wenn sich die Diagonalen in einem Viereck halbieren und senkrecht aufeinander stehen,
sind alle vier Seiten gleich lang und die vier Innenwinkel rechtwinklig.Korregiere hier, die Winkel müssen nicht rechtwinklig sein.--RicRic 14:29, 3. Jan. 2012 (CET)--RicRic 22:29, 23. Dez. 2011 (CET)
Also dann stelle ich mal meinen Lösungsvorschlag ein: An dieser Stelle noch angemerkt: Ich bin für jeden Komentar dankbar, ich weiß dass x Leute dies hier lesen, also bitte auch kurz komentieren, z.B. cool, oder kann ich nicht nachvollziehen, oder könnte da ein Fehler sein, oder sehe ich anders......; Wir wollen doch alle gute Lehrer werden :-)
Def.:Eine Raute ist ein Viereck mit vier gleich langen Seiten.
Implikation: Wenn ein Viereck vier gleich lange Seiten hat, stehen die Diagonalen Senkrecht aufeinander und halbieren sich.
Vorr.: Es sei  ein Viereck mit den Seiten a,b,c,d mit:
ein Viereck mit den Seiten a,b,c,d mit: 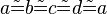
Beh.: 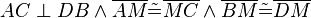
Beweis:
| Überschrift 1 | Überschrift 2 |
|---|---|
(1)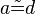 |
Vorr |
(2)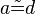 |
Vorr |
(3)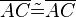 |
trivial |
(4)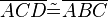 |
SSS, (1),(2),(3) |
(5)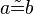 |
Vorr |
(6)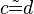 |
Vorr |
(7)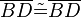 |
trivial |
(8)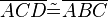 |
SSS, (5),(6),(7) |
(9)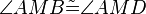 |
(4) |
(10)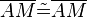 |
trivial |
(11)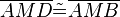 |
SWS, (9),(10),(1) |
(12)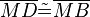 |
(11) |
(13)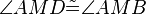 |
(11) |
(14)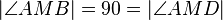 |
(13), Nebenwinkel, Sublementaxiom |
(15)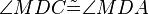 |
(8) |
(16)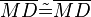 |
trivial |
(17)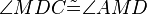 |
SWS (15),(16),(6) |
(18)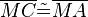 |
(17) |
(19)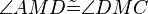 |
(17) |
(20)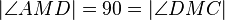 |
(19),(17), Nebenwinkel, Sublementaxiom |
(21)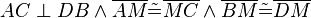 q.e.d. q.e.d. |
(14),20),(18),(12), Def Senkrecht |
Umkehrung: Wenn in einem Viereck die Diagonalen senkrecht aufeinander stehen und sich halbieren, dann hat das Viereck vier konguente Seiten.
Vorr.: Es sei  ein Viereck mit:
ein Viereck mit: 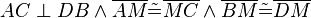
Beh.: Für die Seiten a,b,c,d von  gilt:
gilt: 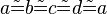
Beweis:
| Überschrift 1 | Überschrift 2 |
|---|---|
(1)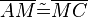 |
Vorr. |
(2)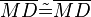 |
trivial |
(3)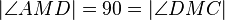 |
Def. Senkrecht, konguente Nebenwinkel, sind rechte Winkel |
(4)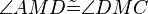 |
(1),(2),(3), SWS |
(5)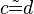 |
(4) |
(6)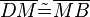 |
Vorr. |
(7)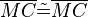 |
trivial |
(8)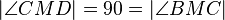 |
Def. Senkrecht, konguente Nebenwinkel, sind rechte Winkel |
(9)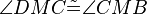 |
(5),(6),(7), SWS |
(10)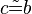 |
(9) |
(11)analog für 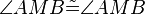 |
|
(12) gilt: gilt: 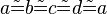 q.e.d. q.e.d. |
(5),(10),(11) |
Kriterium: Genau dann wenn sich ein einem Viereck  die Diagonalen halbieren und Senkrecht aufeinander stehen, sind in diesem Viereck
die Diagonalen halbieren und Senkrecht aufeinander stehen, sind in diesem Viereck  alle vier Seiten konguent zueinander.--RicRic 09:34, 8. Jan. 2012 (CET)
alle vier Seiten konguent zueinander.--RicRic 09:34, 8. Jan. 2012 (CET)
!!!!Müsste es in Schritt 4 und 9 nicht heißen, dass die Dreiecke kongruent sind?? Ansonsten finde ich die Lösung sehr anschaulich!!!!--Snake luzifer 13:10, 8. Jan. 2012 (CET) Stimmt! Habe ich im Formeleditor wohl verhaspelt. Danke.--RicRic 19:25, 9. Jan. 2012 (CET)
- Weihnachtliche Spezialaufgabe:
Ich mache mal den Anfang:) --Tutorin Anne 23:14, 14. Dez. 2011 (CET) :
Wie fängt man den Weihnachtsmann?
Lösungsvorschläge:
1. Die geometrische Methode:
Man stelle einen zylindrischen Käfig im Wald auf eine schneebedeckte Lichtung:
Fall 1: Der Weihnachtsmann ist innerhalb des Käfigs. Dieser Fall ist trivial.
Fall 2: Der Weihnachtsmann ist außerhalb des Käfigs. Dann stelle man sich in den Käfig und führe eine Inversion* an den Käfigwänden durch. So gelangt der Weihnachtsmann in den Käfig und man selbst nach draußen. Man achte darauf, dass man sich nicht in die Mitte des Käfigs stellt, da man sonst im Unendlichen verschwindet.
2. Die Projektionsmethode:
Ohne Beschränkung der Allgemeinheit nehmen wir an, dass die Erde eine Ebene ist. Wir projizieren nun diese Ebene auf eine Gerade, die durch den Käfig läuft, und diese Gerade auf einen Punkt im Käfig. Damit gelangt der Weihnachtsmann in den Käfig.
(Quelle und weitere Methoden unter: www.unterhaltungsspiele.com)
Inversion*: ist eine Spiegelung am Kreis, nicht ganz vergleichbar mit einer Geradenspiegelung, weiters unter: http://de.wikipedia.org/wiki/Inversion_%28Geometrie%29
Alsoo diese Spezialaufgabe halte ich erst für lösbar, wenn mann mindestens 3 Glühwein .... vorher lohnt sich der Gedanke kaum...--RicRic 21:17, 21. Dez. 2011 (CET)

