Übung Aufgaben 3 P (SoSe 12)

Aufgabe 3.1

Beweisen Sie mit Hilfe einer Wahrheitstabelle:

$(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)$

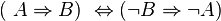
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Lösung von Aufgabe 3.1_P (SoSe_12)

Aufgabe 3.2

a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert.
b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.
Lösung von Aufgabe 3.2_P (SoSe_12)

Aufgabe 3.3

Unter einer Konventionaldefinition versteht man eine Definition, die in der Form "Wenn-Dann" formuliert wurde.
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
Lösung von Aufgabe 3.3_P (SoSe_12)

Aufgabe 3.4

Geben Sie eine Konstruktionsvorschrift (genetische Definition) für die Winkelhalbierende eines gegebenen Winkels an.
Lösung von Aufgabe 3.4_P (SoSe_12)

Aufgabe 3.5

Handelt es sich im Folgenden um einen Satz oder um eine Definition?
Der Mittelpunkt des Umkreises eines Dreiecks ist der Schnittpunkt der Mittelsenkrechten dieses Dreiecks.
Erläutern Sie in diesem Zusammenhang den Unterschied zwischen einer Definition und einem Satz.
Lösung von Aufgabe 3.5_P (SoSe_12)

Aufgabe 3.6

Satz: Gegeben sei ein Dreieck $\overline{ABC}$ in einer Ebene E und eine Gerade g in dieser Ebene, die keine der drei Punkte A, B und C enthält. Wenn g die Strecke $\overline{BC}$ schneidet, so schneidet sie auch entweder die Strecke $\overline{AC}$ oder die Strecke $\overline{AB}$.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 3.6_P (SoSe_12)

Aufgabe 3.7

Gegeben sei folgende Äquivalenz: Der Abstand zweier Punkte A und B ist genau dann 0, wenn A und B identisch sind.
a) Formulieren Sie die beiden Implikationen, die in dieser Aussage stecken.
b) Wie lautet jeweils die Kontraposition der beiden Implikationen?
c) Wie lauten die beiden Annahmen, wenn Sie diese Implikationen jeweils durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 3.7_P (SoSe_12)