Lösung von Aufgabe 5.1 S (SoSe 12)

Die Aufgabe

Satz:

Von drei paarweise verschiedenen Punkten $\ A, B$ und $\ C$ ein und derselben Geraden $\ g$ liegt genau einer zwischen den beiden anderen.

Beweisen Sie diesen Satz.

Lösungsvorschlag 1

          Vor.: koll(A,B,C) und liegen auf einer Geraden g
          Beh.: |AB| + |BC|  = |AC|
          Ann.: Zw(A,B,C) $\Rightarrow$ Zw(C,B,A) $\wedge$ A,B,C $\in$ g

      dir.Bew.: Zw(A,B,C)
                |AB| + |BC|  = |AC|
                |CB| + |BA|  = |CA|
                $\Rightarrow$ Zw(A,B,C)
                $\Rightarrow$ koll(A,B,C)
                $\Rightarrow$ A,B,C $\in$ g

Der Satz stimmt: B liegt zwischen A und C --Gilmore 18:34, 17. Mai 2012 (CEST)

Kommentar zu Lösungsvorschlag 1 von --*m.g.* 18:48, 17. Mai 2012 (CEST)

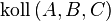• $\operatorname{koll}\left(A,B,C\right)$ bedeutet, dass die drei Punkte auf ein und derselben Geraden liegen, alles was hinter dem und kommt ist somit "doppelt gemoppelt", also weglassen.
• Die Behauptung: $\left|AB\right|+\left|BC\right|=\left|AC\right|$ spiegelt die Aussage des Satzes nicht korrekt wider:

Der Satz hat eigentlich zwei Behauptungen:

1. Überhaupt einer der drei kollinearen Punkte liegt zwischen den beiden anderen (Existenz),
2. Kein weiterer Punkt liegt zwischen den beiden anderen. Konkreter: Wenn wir etwa mit $B$ den Punkt gefunden hätten der von den drei Punkten zwischen den beiden anderen (also in diesem Fall zwischen $A$ und $C$) liegt, dann liegt weder $C$ zwischen $A$ und $B$ noch $A$ zwischen $B$ und $C$ (Eindeutigkeit).