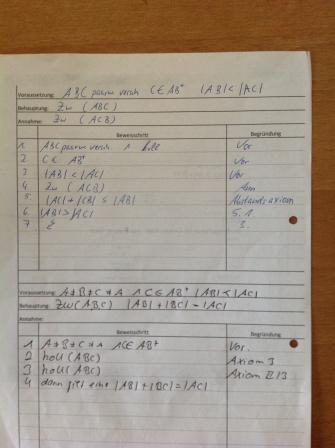
Lösung von Aufgabe 5.3 S (SoSe 12)

Zeigen Sie, dass für drei paarweise verschiedene Punkte $\ A, B$ und $\ C$ gilt:
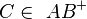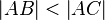Wenn $C \in \ AB^{+}$ und $\left| AB \right| < \left| AC \right|$ dann gilt $\operatorname Zw (A, B, C)$

ich habe Schwierigkeiten das Plus beim B zu interpretieren. Ist Zw. (ABC) eine fertige Aussage?--KeinKurpfälzer 17:09, 21. Mai 2012 (CEST)

Gut, dass Sie fragen. 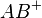$AB^{+}$ ist die Halbgerade, die bei A beginnt und in Richtung B verläuft. Werden wir am Donnerstag behandeln. Und Ihre zweite Frage: Ja, $\operatorname Zw (A, B, C)$ ist eine fertige Aussage. In Worten: B liegt zwischen A und C.--Buchner 10:28, 22. Mai 2012 (CEST)

--H2O 18:58, 21. Mai 2012 (CEST)

Was mache ich	Warum darf ich das?
C Element ABplus	Voraussetzung
koll(A,B,C)	(1)
AB| + |BC| = |AC|; |BC| + |CA| = |BA|; |BA| + |AC| = |BC	Zwischenrelation, (2)
Zw(A,B,C) v Zw(A,C,B) v Zw(B,A,C)	Zwischenrelation, (3)

Nun ist gezeigt, dass eine der Zwischenrelationen gilt (Existenz).
Frage: Habe ich zwei Möglichkeiten?
1.:
Ich zeige, dass Zw(B,A,C) (1. Annahme) und dass Zw(A,C,B) (2. Annahme) nicht gilt.
2.:
Ich zeige, dass zwei Zwischenrelationen nicht gelten.
Ich bin der Meinung, dass die erste Möglichkeit als einzige möglich sein müsste, weil wir ja konkret beweise müssen, dass B zwischen A und C liegt.
Oder muss ich beide Annahmen zum Widerspruch führen?
--RitterSport 15:01, 30. Mai 2012 (CEST)

Anmerkungen von Buchner

Ich stimme Ihnen absolut zu, RitterSport. Sie müssen zeigen, dass weder Zw(B,A,C) noch Zw(A,C,B) gilt.Gemeinsam mit dem Wissen, dass auf jeden Fall eine der drei Gleichungen, d.h. eine der Zwischenrealtionen, gelten muss, haben Sie dann die Aufgabe gelöst. H2O hat schon durch Widerspruchsbeweis Zw (A,C,B) ausgeschlossen- der Beweis ist richtig. Um Zw (B,A,C) auszuschließen brauchen Sie eigentlich keinen großen Beweis- ein paar erklärende Worte genügen. Viel Erfolg!--Buchner 15:57, 31. Mai 2012 (CEST)

Wieso muss ich zeigen, dass nur eine gilt, und dann, dass Zw(A,B,C) gilt? Ist es nicht ausgeschlossen, dass mehr gelten, wenn Zw(A,C,B) und Zw(B,A,C) nicht gelten?--RitterSport 11:34, 1. Jun. 2012 (CEST)
Also wenn man zeigt, dass Zw(B,A,C) und Zw(B,C,A) nicht gelten und man weiß, dass eine der drei Zwischenrelationen gilt, dann hat man gezeigt, dass Zw(A,B,C) gilt.--Tutor Andreas 12:18, 19. Jun. 2012 (CEST)

Zw (B,A,C) kann nicht gelten, da nach Voraussetzung 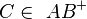$C \in \ AB^{+}$ gelten muss. Bei Zw (B,A,C) liegt C aber auf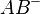$\ AB^{-}$.. Widerspruch zur Voraussetzung.--Tchu Tcha Tcha 17:12, 19. Jun. 2012 (CEST)