Lösung von Aufgabe 10.6 S
Lösungsversuch Nummero6/Tchu Tcha Tcha:
a)Parallelogramme.
Def. (Parallelogramm): Ein Viereck, bei dem die gegenüberliegenden Seiten jeweils gleichlang sind, nennt man Parallelogramm.
b)Wenn ein Viereck ein Parallelogramm ist, dann halbieren sich seine Diagonalen.
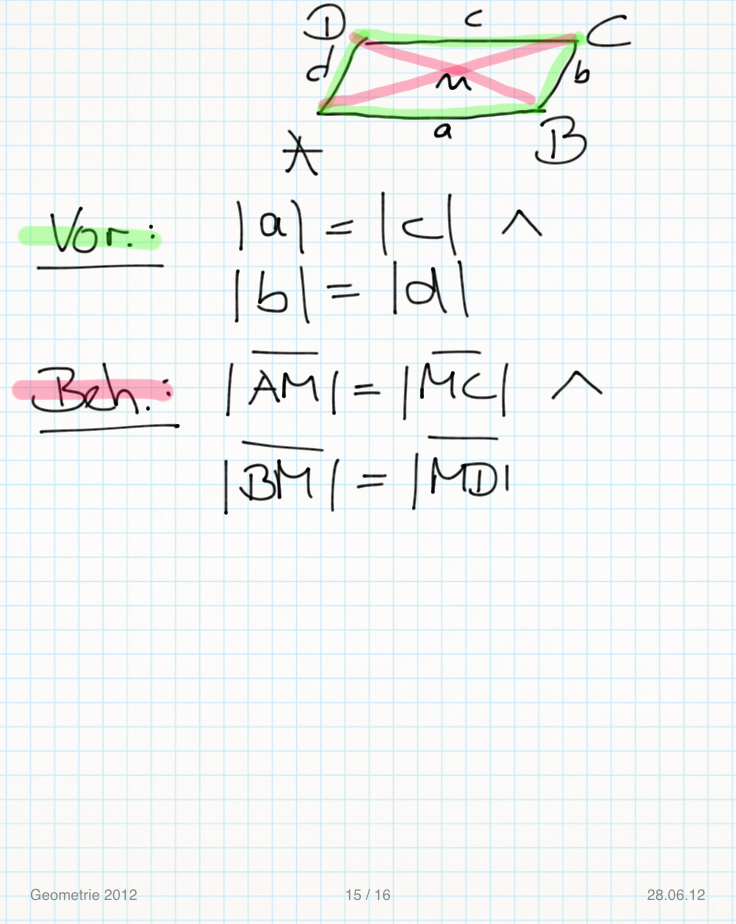
(1) 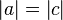 // Voraussetzung
// Voraussetzung
(2) 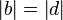 // Voraussetzung
// Voraussetzung
(3) 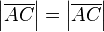 // trivial
// trivial
(4) 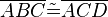 // (1-3), SSS
// (1-3), SSS
(4a) 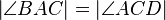 // (4), Dreieckskongruenz
// (4), Dreieckskongruenz
(5) 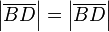 // trivial
// trivial
(6) 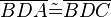 // (1), (2), (5), SSS
// (1), (2), (5), SSS
(6a) 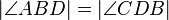 // (6), Dreieckskongruenz
// (6), Dreieckskongruenz
(7) 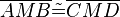 // (1), (4a), (6a), WSW
// (1), (4a), (6a), WSW
(8) 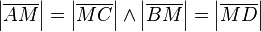 // (7), Dreieckskongruenz
// (7), Dreieckskongruenz
qed
--Tchu Tcha Tcha 18:55, 28. Jun. 2012 (CEST)
Eine Kleinigkeit sollte man noch verändern, aber ansonsten völlig nachvollziehbar und korrekt.
Kleinigkeit:
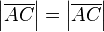 hier entweder
hier entweder 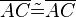 ODER
ODER 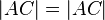 . Das kommt mehrmals im Beweis vor und sollte noch verbessert werden.--Tutor Andreas 19:47, 1. Jul. 2012 (CEST)
. Das kommt mehrmals im Beweis vor und sollte noch verbessert werden.--Tutor Andreas 19:47, 1. Jul. 2012 (CEST)
OK. Ich habe das kongruent Zeichen (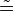 ) nicht gefunden :-)
) nicht gefunden :-)
Wäre diese Form auch nicht korrekt??

--Tchu Tcha Tcha 00:48, 2. Jul. 2012 (CEST)
Es ist eigentlich doppelt gemoppelt und es ist auch nicht definiert, aws das bedeuten soll. Was ist denn der Betrag einer Strecke? --Tutor Andreas 11:01, 10. Jul. 2012 (CEST)
Lösungsversuch: (ich entschuldige mich, dass ich die Zeichen wie Überstrich bei Stecken immer noch nicht kann, aber hab im Moment einfach anders zu tun, also bitte einfach ignorieren, ihr wisst ja wies gemeint ist ;)
b) Vor: Viereck ist Parallelogramm
Beh: Diagonalen halbieren sich
Bew.: zz. AM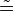 CM ; BM
CM ; BM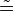 MD
MD
o.B.d.A (1) a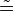 c ; d
c ; d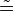 b; BD
b; BD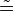 BD \ Vor , trivial
BD \ Vor , trivial
(2) Dreieck ABD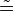 Dreieick CBD \(1), SSS
Dreieick CBD \(1), SSS
(3) Strecke zum Mittelpunkt von BD von A gleich groß wie von C, also AM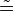 CM \ (2), muss hier sonst noch was hin?
CM \ (2), muss hier sonst noch was hin?
(4) Die Diagonale BD schneidet also AC im Mittelpunkt, wegen o.B.d.A. hier schon q.e.d. \(3)
--Monsta 18:14, 2. Jul. 2012 (CEST)

