Lösung von Aufgabe 5.3 P (SoSe 13)

Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
$\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace$

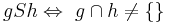
• reflexiv , weil g vereinigt mit g ist ungleich leere Menge
• symmetrisch, weil aus g vereinigt mit h = h vereinigt mit g folgt wegen der Eigenschaft und Schnittmenge
• NICHT transitiv
  • Warum soll die Relation nicht transitiv sein?--Tutorin Anne 16:46, 26. Mai 2013 (CEST)
    • Gegenbeispiel: Wenn g mit h einen Schnittpunkt gemeinsam haben und g mit i ( eine weitere Gerade) einen Schnittpunkt gemeinsam haben, muss nicht unbedingt die Gerade h mit der Gerade i einen gemeinsam Schnittpunkt besitzen. --Blumenkind 18:11, 27. Mai 2013 (CEST)Blumenkind 27. Mai 18:11
      • Und wie sieht so ein Gegenbeispiel genau aus? Warum sollten sie keinen gemeinsamen Schnittpunkt haben?--Tutorin Anne 18:56, 2. Jun. 2013 (CEST)

Bedeutet der "genau dann wenn" Pfeil nicht eh das es eine Äquivalenzrelation ist? Dann wäre sie reflexiv, symmetrisch und transitiv ist. --Wüstenfuchs 19:18, 9. Jul. 2013 (CEST)