Lösung von Zusatzaufgabe 6.2P (SoSe 13)
Aus Geometrie-Wiki
Version vom 18. Juli 2013, 20:16 Uhr von Nolessonlearned (Diskussion | Beiträge)
Beweisen Sie: Es sei  mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt genau eine der folgenden Zwischenrelationen:  oder
oder 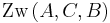 oder
oder 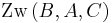 .
.
Voraussetzung: koll(A,B,C) mit A,B,C paarweise verschieden
Behauptung: Zw(A,B,C) oder Zw(B,A,C), oder Zw(A,C,B)
1) ∃g: A,B,C ∈ g
Begründung: Voraussetzung, Def. kollinear
2) Strecke AC mit |AB| + |BC| = |AC| ∈ g
oder Strecke BC mit |BA| + |AC| = |BC| ∈ g
oder Strecke AB mit |AC| + |CB| = |AB| ∈ g
Begründung: (1); Def. Zwischen, Eigenschaft Gerade
3) |AB| + |BC| = |AC| ≔ Zw(A,B,C)
|BA| + |AC| = |BC| ≔ Zw(B,A,C)
|AC| + |CB| = |AB| ≔ Zw(A,C,B)
Begründung: (1); (2); q.e.d.
--Nolessonlearned 21:16, 18. Jul. 2013 (CEST)

