Lösung von Zusatzaufgabe 6.2P (SoSe 13)
Aus Geometrie-Wiki
Beweisen Sie: Es sei  mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt genau eine der folgenden Zwischenrelationen:  oder
oder 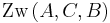 oder
oder 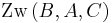 .
.
Voraussetzung: koll(A,B,C) mit A,B,C paarweise verschieden
Behauptung: Zw(A,B,C) oder Zw(B,A,C), oder Zw(A,C,B)
1) ∃g: A,B,C ∈ g
Begründung: Voraussetzung, Def. kollinear
2) Strecke AC mit |AB| + |BC| = |AC| ∈ g
oder Strecke BC mit |BA| + |AC| = |BC| ∈ g
oder Strecke AB mit |AC| + |CB| = |AB| ∈ g
Begründung: (1); Def. Zwischen, Eigenschaft Gerade
3) |AB| + |BC| = |AC| ≔ Zw(A,B,C)
|BA| + |AC| = |BC| ≔ Zw(B,A,C)
|AC| + |CB| = |AB| ≔ Zw(A,C,B)
Begründung: (1); (2); q.e.d.
--Nolessonlearned 21:16, 18. Jul. 2013 (CEST)
- Das ist nur der erste TEil des Beweises und der ist eigentlich trivial, das muss nicht so deutlich aufgeschrieben werden. Entscheident ist dass es in der Dreiecksungleichung steht (Begründung!). Der zweite Teil ist wichtig: Beweise es gilt nur EINE Zwischenrelation. Tipp: Indirekter Beweis. Annahme: zwei Zwischenrelationen gelten. --Tutorin Anne 22:00, 18. Jul. 2013 (CEST)

