Der Basiswinkelsatz WS 16 17
Aus Geometrie-Wiki
Version vom 15. Dezember 2016, 17:59 Uhr von Regenbogen (Diskussion | Beiträge)
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VIII.1 : (gleichschenkliges Dreieck)
Ein Dreieck ist dann gleichschenklig, wenn es zwei gleich lange Seiten hat. Diese zwei Seiten nennt man Schenkel, die dritte Seite wird Basis genannt. Die Winkel zwischen Schenkel und Basis heißen Basiswinkel. --Regenbogen (Diskussion) 17:59, 15. Dez. 2016 (CET)
Der Basiswinkelsatz
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: ...
Behauptung: ...
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 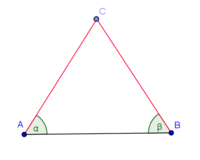
|
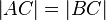
|
ergänzen Sie --- |
| (2) | 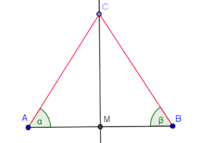
|
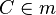 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
--- |
| (3) | |
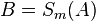
|
--- |
| (4) | |
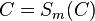
|
--- |
| (5) | |
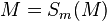
|
--- |
| (6a) | |
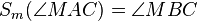
|
--- |
| (6b) | |
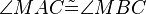
|
--- |

