Beispiele, Gegenbeispiele
Beispiel 1
Wir gehen von der additiven Gruppe der Restklassen modulo 6 aus ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) . .
Die Gruppe besteht aus den folgenden Restklassen: 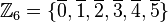
Die Gruppentafel sieht wie folgt aus:
Wir wählen aus 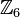 die folgende Teilmenge die folgende Teilmenge 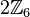 aus: aus:
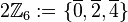
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von ist eine Gruppe und damit eine Untergruppe von ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png)
Beispiel 2
Die Gruppe der Bewegungen
Die Gruppenmitglieder
Unter einer Bewegung  versteht man eine abstandserhaltende Abbildung der Ebene auf sich: versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
Es sei  unsere Ebene. unsere Ebene.
 ist Relation ist Relation
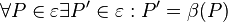
 ist eindeutig und damit Abbildung ist eindeutig und damit Abbildung
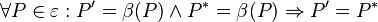
 ist abstandserhaltend ist abstandserhaltend
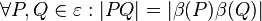
Die Menge aller Bewegungen wollen wir mit 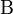 bezeichnen. bezeichnen.
Die Verknüpfung
wir wählen als Verknüpfung auf 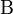 die NAF von Abbildungen und kennzeichnen diese mit die NAF von Abbildungen und kennzeichnen diese mit  . .
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe ist Gruppe
Abgeschlossenheit
Es seien  und und  zwei Bewegungen. zwei Bewegungen.
Wir haben zu zeigen, dass 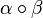 eine Bewegung ist. eine Bewegung ist.
Da die NAF zweier Abbildungen immer eine Abbildung ist, müssen wir nur zeigen dass 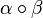 abstandserhaltend ist: abstandserhaltend ist:

| ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) .
.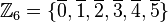




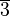
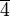
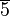
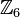 die folgende Teilmenge
die folgende Teilmenge 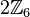 aus:
aus: 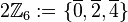
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von
ist eine Gruppe und damit eine Untergruppe von  versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
versteht man eine abstandserhaltende Abbildung der Ebene auf sich: unsere Ebene.
unsere Ebene.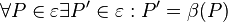
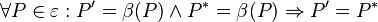
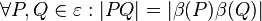
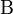 bezeichnen.
bezeichnen.
 .
.
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe
ist Gruppe und
und 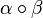 eine Bewegung ist.
eine Bewegung ist.

