Lösung von Aufgabe 1.4 (SoSe 20)

Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen.

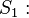$S_1:$ Menge aller Vierecke mit vier kongruenten Winkeln

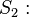$S_2:$ Menge aller Vierecke mit gleich langen, einander halbierenden Diagonalen

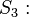$S_3:$ Menge aller Vierecke mit zwei Paaren paralleler Gegenseiten und einem rechten Winkel

- S1: Quadrat, Rechteck, Raute - S2: Quadrat, Rechteck, Raute, Parallelogramm - S3: Quadrat, Rechteck - S3 ist Teilmenge von S1 und diese ist Teilmenge von S2. --Elisa R. (Diskussion) 18:50, 18. Apr. 2020 (CEST)

Ich sage $S_1$ = $S_2$ = $S_3$ Aber warum?  --Tutorin Laura (Diskussion) 12:16, 19. Apr. 2020 (CEST)

-zu S1: Die Raute hat doch aber 2 mal 2 gegenüberliegende Winkel, die kongruent zueinander sind, nicht aber 4 kongruente Winkel? -zu S2: Die Raute hat aber doch nicht zwingend 2 gleich lange Diagonalen? --Coronaldinho (Diskussion) 18:19, 20. Apr. 2020 (CEST)

Das stimmt. Gut aufgepasst. Wie sieht es bei S2 mit dem Parallelogramm aus?   --Tutorin Laura (Diskussion) 23:02, 20. Apr. 2020 (CEST)

-Parallelogramm auch nicht zwingend gleich lange Diagonalen.--Coronaldinho (Diskussion) 12:08, 21. Apr. 2020 (CEST)