Diskussion:Lösung von Aufgabe 13.5
Aus Geometrie-Wiki
Version vom 20. Juli 2010, 17:49 Uhr von Löwenzahn (Diskussion | Beiträge)
Zur Lösung von Löwenzahn:
- Muss es nicht heißen
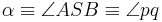 ? Aber mal wieder nur Haarspalterei, vermutlich.
? Aber mal wieder nur Haarspalterei, vermutlich.
- Und: braucht man Schritt (V) bis (VII). Es reicht doch die Dreieckskongruenz aus, die man aus SWS und (II), (III) und (IV) ableiten kann.
- Und: Du meinst in Schritt (X) sicher das Richtige, nur fehlt die Form, aus der abzusehen ist, dass
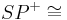 Winkelhalbierenden von
Winkelhalbierenden von 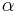 .
.
- "Es seien
 ,
,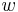 und
und 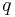 drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt
drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt  . Die Halbgerade
. Die Halbgerade 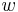 ist die Winkelhalbierende des Winkels
ist die Winkelhalbierende des Winkels 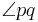 , wenn
, wenn 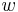 im Inneren von
im Inneren von 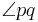 liegt und die beiden Winkel
liegt und die beiden Winkel 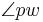 und
und 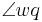 dieselbe Größe haben."
dieselbe Größe haben."
- Besser vielleicht:
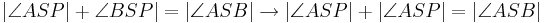
- Muss es nicht heißen
--Heinzvaneugen 16:18, 20. Jul. 2010 (UTC)
Kommentar --Löwenzahn 16:42, 20. Jul. 2010 (UTC):
- Deinen ersten Punkt verstehen ich nicht Heinzvaneugen... ist das nicht das gleiche, ob ich nun drei Striche, oder einen davon geschwungen mache???
- Ich habe versucht über SSW zu argumentrieren, und da muss doch vorher gezeigt werden, dass der größere Winkel, der größeren Seite etc... geht der Satz auch über SWS?
- Ich habe mit "
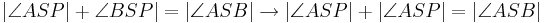 " auch gezeigt, dass
" auch gezeigt, dass 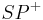 im Inneren liegt, oder?!
im Inneren liegt, oder?!

