12
Aus Geometrie-Wiki
Version vom 16. Januar 2012, 08:05 Uhr von RicRic (Diskussion | Beiträge)
Beweisen Sie Satz VII.6 b
- Wenn ein Punkt
 zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke  gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten  und
und  ein und denselben Abstand.
ein und denselben Abstand.
- Wenn ein Punkt
Vor: 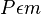 ; m ist Mittelsenkrechte der Strecke
; m ist Mittelsenkrechte der Strecke 
Beh: 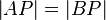
1. 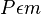 --> Vor.
--> Vor.
2. 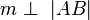 und
und 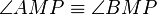 --> 1, Def Mittelsenkrechte, Def senkrecht, Def rechter Winkel
--> 1, Def Mittelsenkrechte, Def senkrecht, Def rechter Winkel
3. 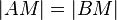 --> 2, Existenz Mittelpunkt
--> 2, Existenz Mittelpunkt
4. 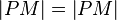 --> trivial, 1
--> trivial, 1
5. Dreiecke 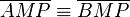 --> 2,3,4, SWS
--> 2,3,4, SWS
6. 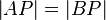 --> 5, Def Dreieckskongruenz
--> 5, Def Dreieckskongruenz
was zu beweisen war. --Cmhock 13:32, 15. Jan. 2012 (CET)
Halte ich für richtig, habe ich im Prinzip genauso.--RicRic 08:05, 16. Jan. 2012 (CET)

