12
Aus Geometrie-Wiki
Version vom 29. Januar 2012, 18:52 Uhr von Phhd mat (Diskussion | Beiträge)
Beweisen Sie: Die Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt.
Siehe Skizze: [[1]]
Behauptung: 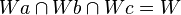
Wir betrachten zunächst 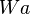 und
und 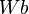 :
:
1. 
2. 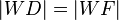 nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
3. 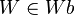
4. 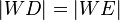 nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
5. 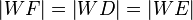 nach 2. und 3.
nach 2. und 3.
Nun kommmen wir zu 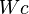
6. 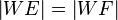 nach 5.
nach 5.
7. 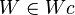 nach Umkehrung Lemma 1.3
nach Umkehrung Lemma 1.3
8. 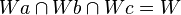 nach 1., 3. und 7.
nach 1., 3. und 7.
--Phhd mat 18:52, 29. Jan. 2012 (CET)

