Lösung von Aufg. 14.3 WS 11/12
Aus Geometrie-Wiki
Beweisen Sie: Die Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt.
Siehe Skizze: [[1]]
Behauptung: 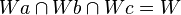
Wir betrachten zunächst 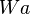 und
und 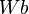 :
:
1. 
Wenn du hier einen Punkt W festlegst, musst du gleich beschreiben, wie er genau liegen muss Im Nachhinein (schritt 3) ist es nicht möglich festzulegen, dass er auch auf Wb liegt.--Tutorin Anne 14:58, 1. Feb. 2012 (CET)
2. 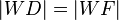 nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
3. 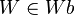
4. 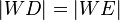 nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
nach Lemma 1.3 (Abstand Punkt zur Winkelhalbierende)
5. 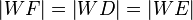 nach 2. und 3.
nach 2. und 3.
Nun kommmen wir zu 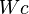
6. 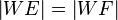 nach 5.
nach 5.
7. 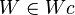 nach Umkehrung Lemma 1.3
nach Umkehrung Lemma 1.3
8. 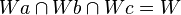 nach 1., 3. und 7.
nach 1., 3. und 7.
--Phhd mat 18:52, 29. Jan. 2012 (CET)
Gut. Ich kann den Beweis nachvollziehen. Achte noch darauf, dass du bei der Begründung alle nötigen vorigen Schritte nennst. Falls einer nicht genannt wird, hättest du ihn auch nicht schreiben brauchen. --Tutorin Anne 14:58, 1. Feb. 2012 (CET)
Das einzige was ich nun nicht verstehe, ist die Begründung Lemma 1.3? Was sagt das Lemma 1.3 aus? Kann ich auch Winkelhalbierendenkriterium als Begründung schreiben?

