Die Eigenschaften der Proportionalität nach Fricke
Inhaltsverzeichnis |
Vervielfachungseigenschaft
Wenn der x-Wert vervielfacht wird, wird der y-Wert mit dem gleichen Faktor vervielfacht
oder
wenn x2=b·x1 dann y2=b·y1
oder
x2 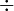 x1 = y2
x1 = y2 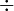 y1
y1
--Löwenzahn 18:36, 5. Nov. 2011 (CET)
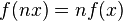 --*m.g.* 16:46, 13. Nov. 2011 (CET)
--*m.g.* 16:46, 13. Nov. 2011 (CET)
Summeneigenschaft
"Die Summe zweiter Größen des einen Bereichs entspricht immer die Summe der zugeordneten Größen des anderen Bereichs" (Fricke)
oder
x1 + x2 → y1 + y2
oder
f(x1 + x2) → f(x1) + f(x2)
oder
wenn x1 + x2 = x3 dann y1 + y2 = y3
--Löwenzahn 18:40, 5. Nov. 2011 (CET)
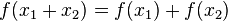 --*m.g.* 16:47, 13. Nov. 2011 (CET)
--*m.g.* 16:47, 13. Nov. 2011 (CET)
Mittelwerteigenschaft
"Dem Mittelwert zweier Größen des einen Bereiches entspricht immer der Mittelwert der zugeordneten Größen des anderen Bereiches" (Fricke)
oder
(x1 + x2) 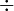 2 → (y1 + y2)
2 → (y1 + y2) 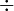 2
2
--Löwenzahn 18:46, 5. Nov. 2011 (CET)
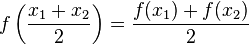 --*m.g.* 16:53, 13. Nov. 2011 (CET)
--*m.g.* 16:53, 13. Nov. 2011 (CET)
Ist die Mittelwerteigenschaft notwendig und hinreichend für die Proportionalität? Meiner Meinung nach nicht, denn sie gilt auch allg. für andere lineare Funktionen. Stimmt das?
Würde dir zustimmen. Die Mittelwerteigenschaft trifft auch bei einer linearen Funktion zu (z.B. y=x+1), daher ist die Eigenschaft notwendig aber nicht hinreichend für Proportionalität.--Löwenzahn 12:53, 1. Feb. 2012 (CET)
Quotienteneigenschaft
"Die Quotienten einander zugeordneter Größen sind stets gleich groß" (Fricke)
oder
y=p·x
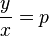 (p=const)
(p=const)
oder
x=p·y
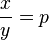 (p=const)
(p=const)
--Löwenzahn 14:54, 10. Nov. 2011 (CET)
Abstandseigenschaft
"Gleichabständige Maßzahlen des einen Größenbereiches entsprechen auch immer gleichabständigen Maßzahlen des anderen Größenbereiches"(Fricke)
oder
x2 - x1 = x4 - x3 → y2 - y1 = y4 - y3
--Löwenzahn 14:54, 10. Nov. 2011 (CET)
Differenzenqoutienteneigenschaft
"Die Quotienten der Differenzen zweier Größen des einen Bereiches sind zu den entsprechenden Differenzen des anderen Größenbereiches immer gleich"(Fricke)
oder
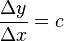 (c=const)
(c=const)
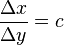 (c=const)
(c=const)
--Löwenzahn 15:09, 10. Nov. 2011 (CET)
Auch diese Eigenschaft ist meiner Meinung nach zwar notwendig, aber nicht hinreichend für das Vorliegen einer Proportionalität, oder?
Würde dir auch hier zustimmen. Wie bei der Mittelwerteigenschaft ist die Differenzenquotienteneigenschaft notwendig aber nicht hinreichend für Proportionalität. Wieder am Beispiel y=x+1 deutlich, da hier die Differenzenquotienteneigenschaft zutrifft.--Löwenzahn 12:55, 1. Feb. 2012 (CET)

