12
Inhaltsverzeichnis |
Videos
Peripheriewinkelsatz
Begriff des Peripheriewinkels
Peripheriewinkelsatz
Satz des Thales
Satzfindung
"Beweisen" am Beispiel
Ikonischer Beweis
Definition XIX.1 (Peripheriewinkel)
Der Winkel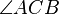 
im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:
Es sei k ein Kreis und pq ein Winkel. Winkel pq ist Peripheriewinkel von k, wenn der Scheitelpunkt C von Winkel pq auf k liegt und p und q den Kreis k jeweils in einem weiteren Punkt A bzw. B schneiden (mit A ungleich B). --Lottta 19:38, 31. Jan. 2012 (CET)
Definition XIX.2 (Zentriwinkel)
Der Winkel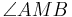 
im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:
Es sei APB ein Peripheriewinkel des Kreises k mit Mittelpunkt M. Der Winkel AMB heißt der zum Peripheriewinkel APB dazugehörige Zentriwinkel. --Lottta 19:40, 31. Jan. 2012 (CET)
Idee des Beweises eines Spezialfalls
Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?
Der Zentri-Peripheriewinkelsatz
ergänzen Sie:
Jeder Peripheriewinkel ist...
Satz XIX.1:(Der Zentri-Peripheriewinkelsatz)
Zentri-Peripheriewinkelsatz: Ein Peripheriewinkel ist immer halb so groß wie sein dazugehöriger Zentriwinkel. --Lottta 19:31, 31. Jan. 2012 (CET)
Der Peripheriewinkelsatz
Satz XIX.2:(Der Peripheriewinkelsatz)
ergänzen Sie:
Alle Peripheriewinkel am Kreis k über der gleichen Sehne sind kongruent zueinander. --Lottta 19:29, 31. Jan. 2012 (CET)
