Peripheriewinkelsatz und Zentriwinkel-Peripheriewinkelsatz WS 11/12

Videos

Definition XIX.1 (Peripheriewinkel)

Der Winkel 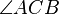$\angle ACB$ im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:

Es sei k ein Kreis und pq ein Winkel. Winkel pq ist Peripheriewinkel von k, wenn der Scheitelpunkt C von Winkel pq auf k liegt und p und q den Kreis k jeweils in einem weiteren Punkt A bzw. B schneiden (mit A ungleich B). --Lottta 19:38, 31. Jan. 2012 (CET)

Definition XIX.2 (Zentriwinkel)

Der Winkel 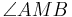$\angle AMB$ im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:

Es sei ACB ein Peripheriewinkel des Kreises k mit Mittelpunkt M. Der Winkel AMB heißt der zum Peripheriewinkel ACB dazugehörige Zentriwinkel. --Lottta 19:40, 31. Jan. 2012 (CET)

Idee des Beweises eines Spezialfalls

Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?

Was ist denn hier mit "Spezialfall" gemeint?? Angewendet wird der starke Außenwinkelsatz (ein Außenwinkel ist so groß wie die beiden nicht anliegenden Innenwinkel zusammen). Aber wieso Spezialfall? Und was ist mit den anderen Fällen??? --Lottta 13:01, 4. Feb. 2012 (CET)

Der Zentri-Peripheriewinkelsatz

ergänzen Sie:
Jeder Peripheriewinkel ist...

Satz XIX.1:(Der Zentri-Peripheriewinkelsatz)

Zentri-Peripheriewinkelsatz: Ein Peripheriewinkel ist immer halb so groß wie sein dazugehöriger Zentriwinkel. --Lottta 19:31, 31. Jan. 2012 (CET)

Der Peripheriewinkelsatz

Satz XIX.2:(Der Peripheriewinkelsatz)

ergänzen Sie:

Alle Peripheriewinkel am Kreis k über der gleichen Sehne sind kongruent zueinander. --Lottta 19:29, 31. Jan. 2012 (CET)