Lösung der Aufgaben zur Mengenlehre (SoSe 12)
Inhaltsverzeichnis |
Mengenlehre
Aufgabe 1
A und B sind identisch. --PippiLotta 09:22, 18. Apr. 2012 (CEST)
Ich würde sagen B ist Teilmenge von A, da A mehr Zahlen besitzt als B. z.B besitzt B die Zahlen 1,2,3,5 .... nicht. Somit ist B Teilmenge von A.--Maliglowka 16:36, 18. Apr. 2012 (CEST)
Die Menge A besitzt die Zahlen 1,3 und 5 auch nicht, weil sie nur gerade natürliche Zahlen besitzt. Deswegen würde ich auch sagen, dass die Mengen identisch sind.
Freut mich, dass hier schon diskutiert wird. Ich fände es gut, wenn jeder seinen Kommentar signieren würde, damit man besser erkennen kann, welcher Kommentar von wem ist.--Tutor Andreas 23:38, 18. Apr. 2012 (CEST)
@Tutor Andreas: habs überlesen aber die Menge A hat ja gerade natürliche Zahlen und da zählt schon die 2 bzw beginnt bei der 2. Die erste natürliche Quadratzahl ist aber 4, somit enthält A alle Zahlen von B, aber B hat nicht die 2. Oder sehe ich da was falsches? --Maliglowka 16:36, 18. Apr. 2012 (CEST)
Aufgabe 2
M1={}
M2={}
M3={-2}
M4={}
M5= 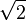
M6={-2}
M1=M2=M4
M3=M6--PippiLotta 09:22, 18. Apr. 2012 (CEST)
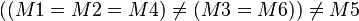 --Maliglowka 16:36, 18. Apr. 2012 (CEST)
--Maliglowka 16:36, 18. Apr. 2012 (CEST)
Aufgabe 3
M1=M3 und M2 ist Teilmenge von M1/M3
Aufgabe 4
N1=N2=N3, alles Rechtecke
Wurzelzeichen? Hier ist eins: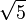 (Quelltext anschauen) Ansonsten in der Hilfe nachsehen:
Formeln_verwenden--*m.g.* 17:17, 18. Apr. 2012 (CEST)
(Quelltext anschauen) Ansonsten in der Hilfe nachsehen:
Formeln_verwenden--*m.g.* 17:17, 18. Apr. 2012 (CEST)

