Lösung von Aufgabe 2.5 S (SoSe 12)
Aus Geometrie-Wiki
Version vom 29. April 2012, 14:53 Uhr von Andreas (Diskussion | Beiträge)
Aufgabe 2.5
Eine Raute sei folgendermaßen definiert: Ein Viereck mit vier kongruenten Seiten heißt Raute.
Sie wollen folgenden Satz beweisen: In einer Raute sind die gegenüberliegenden Seiten parallel zueinander.
a) Formulieren Sie den Satz mit "Wenn... dann..."
- Wenn
 eine Raute ist, dann sind ihre gegenüberliegenden Seiten parallel zueinander.--Caro44 17:03, 27. Apr. 2012 (CEST)
eine Raute ist, dann sind ihre gegenüberliegenden Seiten parallel zueinander.--Caro44 17:03, 27. Apr. 2012 (CEST)
b)Ergänzen Sie:
Voraussetzung:
Behauptung:
Voraussetzung:  ist eine Raute.
Behauptung: Strecke
ist eine Raute.
Behauptung: Strecke 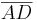 und Strecke
und Strecke  sind parallel zueinander und Strecke
sind parallel zueinander und Strecke  und Strecke
und Strecke 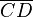 sind parallel zueinander --Caro44 17:11, 27. Apr. 2012 (CEST)
sind parallel zueinander --Caro44 17:11, 27. Apr. 2012 (CEST)
- Hier ein kleiner Tipp für später: Strecken sind nicht parallel, sondern nur die Geraden, die durch die Strecken bestimmt werde.--Tutor Andreas 15:53, 29. Apr. 2012 (CEST)
V:  =
= 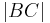 =
= 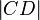 =
= 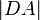
B:  =
= 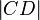 ,
, 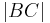 =
= 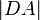 --Oz44oz 18:32, 27. Apr. 2012 (CEST)
--Oz44oz 18:32, 27. Apr. 2012 (CEST)
Bei der Behauptung wird doch von parallel zueinander gesprochen, wieso dann " = " ?
Behauptung : 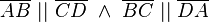
--Funkdocta 15:32, 29. Apr. 2012 (CEST)
- Wie schon oben erwähnt, müsste es eigentlich
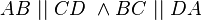 heißen.--Tutor Andreas 15:53, 29. Apr. 2012 (CEST)
heißen.--Tutor Andreas 15:53, 29. Apr. 2012 (CEST)

