Lösung von Aufgabe 2.7 S (SoSe 12)

Aufgabe 2.7

Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz.

1. Wenn $\overline {ABCD}$ vier rechte Innenwinkel hat, dann ist es ein Quadrat.
2. Wenn ein Punkt auf der Hypothenuse eines rechtwinkligen Dreiecks $\overline {ABC}$ liegt, dann ist es der Mittelpunkt des Umkreises des Dreiecks.
3. Wenn sich die Diagonalen eines Vierecks schneiden, dann ist es konvex.
4. Wenn die Symmetrieachsen von $\overline {ABCD}$ durch Geraden eindeutig bestimmt sind, dann liegen die Geraden auf den Diagonalen einer Raute.
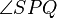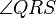5. Wenn die Winkel $\angle {SPQ}$ und $\angle {QRS}$ konruent zueinander sind, dann ist 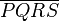$\overline {PQRS}$ ein Parallelogramm.
6. Wenn die Innenwinkelsumme von $\overline {ABC}$ 180° beträgt, dann ist es ein Dreieck.

Passende Äquivalenz bei:
3. Die Diagonalen eines Vierecks schneiden sich genau dann, wenn es konvex ist.
6. $\overline {ABC}$ ist genau dann ein Dreieck, wenn seine Innenwinkelsumme 180° beträgt.

2. Wenn der Mittelpunkt des Umkreises eines Dreiecks auf dessen Hypothenuse liegt, dann ist es ein rechtwinkliges Dreieck.--Goliath 13:49, 29. Apr. 2012 (CEST)

4. Wenn die Geraden Symmetrieachsen der Raute $\overline {ABCD}$ sind, dann werden sie durch die Diagonalen der Raute eindeutig bestimmt.--Goliath 13:49, 29. Apr. 2012 (CEST)