Lösung von Aufgabe 3.3 S (SoSe 12)
Inhaltsverzeichnis |
Aufgabe 3.3
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösungsvorschlag 1
a)
Kontraposition 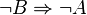
Wenn zwei Geraden nicht nur höchstens einen Punkt gemeinsam haben, dann sind sie identisch.
a) Ich würde vielleicht anstatt "nicht nur höchstens" , "mindestens einen Punkt gemeinsam haben" sagen. Daraus würde ich sagen folgt, dass sie identisch sind oder sich in einem Punkt schneiden, wenn sie wirklich nur einen Punkt dann gemeinsam haben.
b) sehe ich genauso
--Funkdocta 16:23, 6. Mai 2012 (CEST)
b)
Annahme: g und h sind nicht identisch und haben mehr als einen Punkt gemeinsam. --Goliath 16:14, 3. Mai 2012 (CEST)
Lösungsvorschlag 2:
Menge1: g
Menge2: h
Menge1 = Menge 2 oder 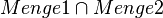 --Hauleri 13:35, 6. Mai 2012 (CEST)
--Hauleri 13:35, 6. Mai 2012 (CEST)

