Übung 7
Aus Geometrie-Wiki
Version vom 3. Juni 2010, 12:42 Uhr von *m.g.* (Diskussion | Beiträge)
Inhaltsverzeichnis |
Aufgabe 7.1
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit  und
und  .
.
Aufgabe 7.2
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit 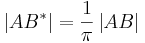 und
und 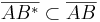 .
.
Aufgabe 7.3
Der Punkt  möge die Strecke
möge die Strecke  derart in die Teilstrecken
derart in die Teilstrecken  und
und  teilen, dass
teilen, dass 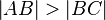 gilt. Beweisen Sie:
gilt. Beweisen Sie:
Wenn 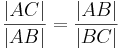 , dann
, dann 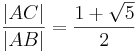 .
.
Aufgabe 7.4 (*)
Was hat Aufgabe 7.3 hiermit zu tun?
Aufgabe 7.5
Definieren noch einmal die Begriffe Halbgerade 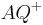 und
und 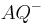 . In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zu den Definitionen
. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zu den Definitionen


