Lösung von Zusatzaufgabe 9.3 S
Aus Geometrie-Wiki
Version vom 25. Juni 2012, 13:47 Uhr von Nummero6 (Diskussion | Beiträge)
Beweisen Sie: Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Existenz und Eindeutigkeit der Winkelhalbierenden
Voraussetzung:
(1) 
Existenz:
zu zeigen: es existiert ein Strahl 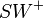 für den gilt:
für den gilt:
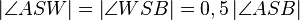
(1)  // Vor.
// Vor.
(2) 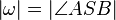 // Winkelmaßaxiom
// Winkelmaßaxiom
(3) Es existiert ein Strahl 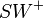 mit W
mit W 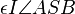 :
: 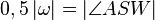 // Winkelkonstruktionsaxiom
// Winkelkonstruktionsaxiom
(4) 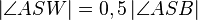 // (3),(2)
// (3),(2)
(5) 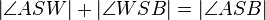 // Winkeladditionsaxiom
// Winkeladditionsaxiom
(6) 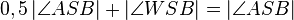 // (4),(5)
// (4),(5)
(7) 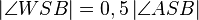 // (6),Rechnen in R
// (6),Rechnen in R
(8) 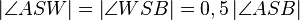 // (4),(7)
// (4),(7)
w.z.b.w.
Eindeutigkeit:
folgt..
--Tchu Tcha Tcha 14:47, 25. Jun. 2012 (CEST)

