Lösung von Aufgabe 6.3

Satz:

Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.

1. Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
2. Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
3. Beweisen Sie den Satz. Hier ein Anfang für den Beweis:

Beweis

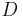Es seien $\ A, B, C$ und $\ D$ drei Punkte, die nicht komplanar sind.

zu zeigen

...

Annahme:

Es gibt drei der Punkte vier Punkte $\ A, B, C, D$, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...

1) Wenn es vier Punkte gibt, bei denen mehr als eine Ebene aufgespannt werden, so befinden sich je drei Punkte nicht auf ein und derselben Geraden.

2) Bei vier zueinander nicht komplanaren Punkten gibt es immer drei nicht kollineare Punkte.

3) Voraussetzung:Es seien A, B, C, D vier Punkte, mit nkomp(A,B,C,D)

Behauptung: Je drei von den Punkten sind nicht kollinear

Annahme: Es gibt drei der vier Punkte, die kollinear sind. Es mögen diese o.B.d.A. die Punkte A,B und C sein.

Beweis:

Beweisschritt	Begründung
1) A,B,C Element von g 2)D nicht Element von g 3) Es Existiert eine Ebene E mit A,B,D 4)komp(A,B,D) 5)Widerspruch zur Voraussetzung, Annahme ist zu verwerfen. analog A,C,D und B,C,D	1)koll(A,B,C) 2)nkoll(A,B,D) o.B.d.A. 3) Axiom I/4 4)Definition komplanar und 3)

--Skellig 22:17, 1. Jun. 2010 (UTC)

--Heinzvaneugen