Lösung von Aufgabe 6.3
Inhaltsverzeichnis |
Satz:
- Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
- Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
- Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
- Beweisen Sie den Satz. Hier ein Anfang für den Beweis:
Lösung: --Schnirch 12:46, 16. Jun. 2010 (UTC)
zu 1) Wenn vier Punkte nicht in einer Ebene liegen, dann gibt es keine drei, die auf einer Geraden liegen.
zu 2) Von vier Punkten, die nicht komplanar sind, gibt es keine drei, die kollinear sind.
zu 3):
Voraussetzung: 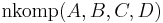
Behauptung: Je drei der Punkte 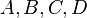 sind nicht kollinear.
sind nicht kollinear.
Annahme: Es gibt drei kollineare Punkte, oBdA sei 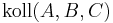
Beweis:
| Schritt | Begründung |
1) Es gibt eine Gerade  mit mit 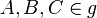
|
Annahme |
Fall 1: 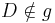
|
|
2) Es gibt eine Ebene  mit mit 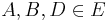
|
Axiom I/4 |
3) 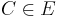
|
(1),(2), Axiom I/5 |
4) 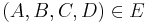
|
(2),(3) |
5) 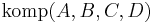
|
(4) |
| Widerspruch zur Voraussetzung | |
Fall 2: 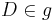
|
|
6) 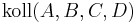
|
|
7) es gibt einen Punkt  , der nicht auf der Geraden , der nicht auf der Geraden  liegt liegt
|
Axiom I/3 |
8) es existiert genau eine Ebene  mit mit 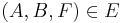
|
Axiom I/4 |
9) mit 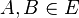 gilt auch gilt auch 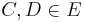
|
Axiom I/5 |
10) 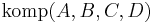
|
(9) |
| Widerspruch zur Voraussetzung |
Annahme ist zu verwerfen! Behauptung stimmt!
vorangegangene Diskussion:
Beweis
- Es seien
 und
und 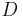 drei Punkte, die nicht komplanar sind.
drei Punkte, die nicht komplanar sind.
- Es seien
zu zeigen
- ...
Annahme:
- Es gibt drei der Punkte vier Punkte
 , die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
- Es gibt drei der Punkte vier Punkte
- Wenn es vier Punkte gibt, bei denen mehr als eine Ebene aufgespannt werden, so befinden sich je drei Punkte nicht auf ein und derselben Geraden.
- Bei vier zueinander nicht komplanaren Punkten gibt es immer drei nicht kollineare Punkte.
- ...
Beweis
Voraussetzung:
Es seien A, B, C, D vier Punkte, mit nkomp(A,B,C,D)
Behauptung:
Je drei von den Punkten sind nicht kollinear
Annahme:
Es gibt drei der vier Punkte, die kollinear sind. Es mögen diese o.B.d.A. die Punkte A,B und C sein.
Beweis:
| Beweisschritt | Begründung |
| 1) A,B,C Element von g 2)D nicht Element von g 3) Es Existiert eine Ebene E mit A,B,D 4)komp(A,B,D) 5)Widerspruch zur Voraussetzung, Annahme ist zu verwerfen. analog A,C,D und B,C,D |
1)koll(A,B,C) 2)nkoll(A,B,D) o.B.d.A. 3) Axiom I/4 4)Definition komplanar und 3) |
--Skellig 22:17, 1. Jun. 2010 (UTC)
Hier noch ein Versuch, das ganze grafisch darzustellen. Sobald drei Punkte kollinear sind, gibt es nur noch eine Ebene, nämlich die mit der jeweiligen Gerade (auf der die drei kollinearen Punkte liegen) und der vierte Punkt.
Man muss sich die Grafik dreidimensional vorstellen, deswegen wurden auch Farben gewählt, die an sich gegen die Genfer Konvention verstoßen.
Der Punkt D (o.B.d.A.) "schwebt" über der Ebene  .
.
--Heinzvaneugen
- Schick! Es wäre natürlich noch schicker, wenn das Ganze tatsächlich dreidimensional wäre. Vielleicht haben Sie Lust, sich an einer dreidimensionalen Modellierung zu versuchen? GeoGebra unterstützt in gewissem Maße Dreidimensionalität - siehe hier --Spannagel 22:06, 7. Jun. 2010 (UTC)
Beweis der Kontraposition
Ich versuche zu beweisen, dass gilt: koll(A,B,C,D) (Das war Quatsch!)
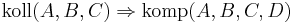
Das ist ja die Kontraposition zu der Aussage: Wenn vier Punkte nicht komplanar sind, dann sind je drei davon nicht kollinear.
1.Fall: 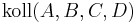
| Schritt | Begründung |
1)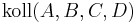
|
Voraussetzung |
2)Es gibt genau eine Gerade  mit mit 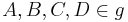
|
(1) |
3)Es gibt eine Ebene  mit mit 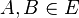
|
Satz I/7 |
4)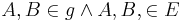
|
(2),(3) |
5)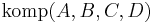
|
(4), Axiom I/5 |
2.Fall: 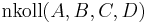
| Schritt | Begründung |
1)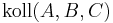
|
Voraussetzung, Punktauswahl o.B.d.A. |
2)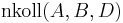
|
Voraussetzung, |
3)Es gibt genau eine Ebene  mit mit 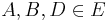
|
(2), Axiom I/4 |
4)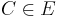
|
(1),(3), Axiom I/5 |
5)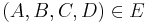
|
(3),(4) |
6)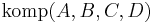
|
(5) |
vgl. Diskussion:Lösung von Aufgabe 6 (aus Woche 5)
--Sternchen 17:37, 4. Jun. 2010 (UTC)
zur Kontraposition
Wir gehen von 4 Punkten  aus.
aus.
noch einmal die Voraussetzung
Es gibt keine Ebene, die alle 4 Punkte  enthält.
Das ist in Worten ausgedrückt, was der Mathematiker kurz als
enthält.
Das ist in Worten ausgedrückt, was der Mathematiker kurz als 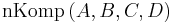 schreibt.
schreibt.
noch einmal die Behauptung
Es gibt keine Gerade, die drei der vier Punkte  enthält.
enthält.
Die Umkehrung
Wenn es keine Gerade gibt, die drei der vier Punkte  enthält, dann sind die vier Punkte
enthält, dann sind die vier Punkte  nicht komplanar.
nicht komplanar.
Die Kontraposition
Wir negieren die Voraussetzung der Umkehrung:
Es gibt keine wird zu Es gibt eine (Doppelte Verneinung: Es gilt nicht, dass es keine Gerade gibt ...)
Also: Es gibt eine Gerade, die drei der vier Punkte  enthält
enthält
Wir negieren die Behauptung der Umkehrung:
die vier Punkte  sind nicht nicht komplanar
sind nicht nicht komplanar
also: die vier Punkte sind komplanar
Alles zusammen: Wenn es eine Gerade gibt, die drei der vier Punkte  enthält, dann sind die vier Punkte
enthält, dann sind die vier Punkte  komplanar.
komplanar.
oder so: (komplanar übersetzt)
Wenn es eine Gerade gibt, die drei der vier Punkte  enthält, dann gibt es (auch) eine Ebene die alle vier Punkte
enthält, dann gibt es (auch) eine Ebene die alle vier Punkte  enthält.
Anders formuliert:
Wenn (o.B.d.A.)
enthält.
Anders formuliert:
Wenn (o.B.d.A.) 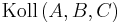 , dann
, dann 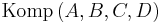
Erkennen Sie den Zusammenhang mit dem indirekten Beweis?
Wichtig: Voraussetzung und Behauptung unseres Satzes (egal ob als Satz oder Umkehrung) sind letztlich negierte Existenzaussagen. Diese Existenzaussagen sind bei der Bildung der Kontraposition zu negieren.
Hinweis: Häufig ist es sinnvoll, beim Beweis von Sätzen die im Satz verwendeten Begriffe (egal ob Objekt- oder Relationsbegriff) zu übersetzen. Im speziellen Fall war das:
-
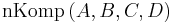 : Es existiert keine Ebene ....
: Es existiert keine Ebene ....
-
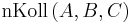 :Es existiert keine Gerade ...
:Es existiert keine Gerade ...
noch ein persönlicher Kommentar: Ich habe lange überlegt, ob ich das jetzt schon schreibe oder noch ein wenig warte. Ich hab mich dann doch entschieden, den Fehler in der Kontraposition möglichst schnell zu verdeutlichen. Lassen Sie sich um Himmels Willen nicht entmutigen. Ihr Beitrag ist für den weiteren Verlauf der Lehrveranstaltung unglaublich wichtig. Wir wissen jetzt, dass wir Existenz-  und Allaussagen
und Allaussagen 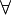 sowie deren Verneinungen deutlicher hervorheben und expliziter behandeln müssen und Ihnen wird es mit Sicherheit nicht noch einmal passieren. Mathematik lernt man nur durch die aktive Auseinandersetzung mit der Materie.
sowie deren Verneinungen deutlicher hervorheben und expliziter behandeln müssen und Ihnen wird es mit Sicherheit nicht noch einmal passieren. Mathematik lernt man nur durch die aktive Auseinandersetzung mit der Materie.
Ich erinnere mich immer wieder an meine erste Mathematikvorlesung überhaupt (Ich kam einen Monat zu spät zum Studium): Es war eine Analysisvorlesung: Existenz und Eindeutigkeit der n-ten Wurzel. Ich dachte ich kapier das nie.
Man merkt an allen Ecken und Enden das Fehlen der Lehrveranstaltung Einführung in die Mathematik (in den 90ger Jahren gab es sowas).
--*m.g.* 17:08, 7. Jun. 2010 (UTC)--*m.g.* 17:08, 7. Jun. 2010 (UTC)
- So leicht lass ich mich bestimmt nicht entmutigen, *m.g.*, aber nicht um des Himmels Willen, sondern weil ich wissen will, was ich falsch gemacht habe. Sonst macht das Ganze doch nicht halb so viel Freude!
- Ich hab jetzt oben was geändert. War es das, was Sie gemeint haben? Ist der Rest richtig?
- --Sternchen 19:29, 7. Jun. 2010 (UTC)

