Diskussion:Lösung von Aufgabe 6
zu 2.
Ich hab unter Schritt (2) vorausgesetzt, dass 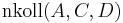 . Ich hab das einfach gemacht, weil ich das Gefühl hatte, dass ich gar nicht weiterkomme bzw. der ganze Beweis keinen Sinn macht, wenn ich nicht das wenigstens voraussetze. Aber ist das überhaupt legitim? --Sternchen 11:13, 21. Mai 2010 (UTC)
. Ich hab das einfach gemacht, weil ich das Gefühl hatte, dass ich gar nicht weiterkomme bzw. der ganze Beweis keinen Sinn macht, wenn ich nicht das wenigstens voraussetze. Aber ist das überhaupt legitim? --Sternchen 11:13, 21. Mai 2010 (UTC)
Ja, in der Tat müssten Sie beweisen, dass ihre Annahme in Schritt 2 korrekt ist. Prima, dass Sie dies erkannt haben! Versuchen Sie den Beweis, er ist nicht schwer!--Schnirch 16:05, 30. Mai 2010 (UTC)
- Es gibt zwei Möglichkeiten, mit dem Problem umzugehen:
- Variante 1: man beweist, dass unter der Voraussetzung
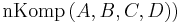 je drei der Punkte
je drei der Punkte  nicht kollinear sind. Oder man macht
nicht kollinear sind. Oder man macht
- Variante 2: eine Fallunterscheidung
- Fall 1: So wie bereits dargestellt : (2.1)
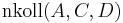
- Fall 1: So wie bereits dargestellt : (2.1)
- Fall 2: (2.2)
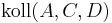
- Fall 2: (2.2)
- Im Fall 2 könnte folgendes passieren:
- Fall 2.1 : Die drei Punkte
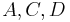 sind paarweise verschieden
sind paarweise verschieden
- Fall 2.2 : Genau zwei der drei Punkte
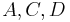 sind identisch. (o.B.d.A.
sind identisch. (o.B.d.A. 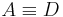 ),
),
- Fall 2.3 : Alle drei Punkte
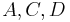 sind identisch.
sind identisch.
- In jedem der drei Fälle hilft Axiom I/7: Es liefert nämlich
- Fälle 2.1 und 2.2: einen weiteren Punkt
 mit
mit 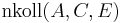 , danach geht es weiter wie in Fall 1,
, danach geht es weiter wie in Fall 1,  übernimmt die Rolle von
übernimmt die Rolle von 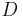
- Fall 2.3 : zwei Punkte
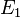 und
und 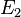 mit
mit 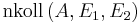 , danach geht es weiter wie in Fall 1,
, danach geht es weiter wie in Fall 1, 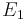 übernimmt die Rolle von
übernimmt die Rolle von  und
und 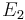 die von
die von 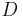 .--*m.g.* 09:34, 2. Jun. 2010 (UTC)
.--*m.g.* 09:34, 2. Jun. 2010 (UTC)
- Fall 2.1 : Die drei Punkte
- Im Fall 2 könnte folgendes passieren:
- Mir ist einiges klar geworden. Mein Schritt 2 folgt also aus Schritt 1, das ist schonmal prima. Und die Tatsache leuchtet mir jetzt auch ein, aber wie beweisen? Da bin ich noch am Überlegen.
- Zu Ihrer Variante 2, *m.g.*: Es gibt ja immer noch einen anderen Punkt, für den die Komplanarität nicht gilt, soweit hab ich's verstanden. Aber wenn ichs nicht besser wüsste, müsste ich ja wieder annehmen, dass der wiederum trotzdem kollinear mit
 und
und  sein könnte. Oder was bringt mir die Fallunterscheidung sonst noch? Ich hab's noch nicht ganz begriffen.--Sternchen 17:20, 3. Jun. 2010 (UTC)
sein könnte. Oder was bringt mir die Fallunterscheidung sonst noch? Ich hab's noch nicht ganz begriffen.--Sternchen 17:20, 3. Jun. 2010 (UTC)
- Zu Ihrer Variante 2, *m.g.*: Es gibt ja immer noch einen anderen Punkt, für den die Komplanarität nicht gilt, soweit hab ich's verstanden. Aber wenn ichs nicht besser wüsste, müsste ich ja wieder annehmen, dass der wiederum trotzdem kollinear mit
Versuch eines Beweises, dass gilt: 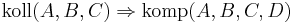
Das ist ja die Kontraposition zu der Aussage: Wenn vier Punkte nicht komplanar sind, dann sind je drei davon nicht kollinear.
1.Fall: 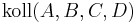
| Schritt | Begründung |
1)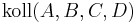
|
Voraussetzung |
2)Es gibt genau eine Gerade  mit mit 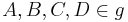
|
(1) |
3)Es gibt eine Ebene  mit mit 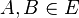
|
Satz I/7 |
4)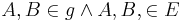
|
(2),(3) |
5)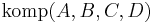
|
(4), Axiom I/5 |
2.Fall: 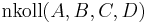
| Schritt | Begründung |
1)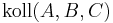
|
Voraussetzung, Punktauswahl o.B.d.A. |
2)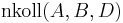
|
Voraussetzung, Punktauswahl o.B.d.A. |
3)Es gibt genau eine Ebene  mit mit 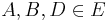
|
(2), Axiom I/4 |
4)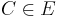
|
(1),(3), Axiom I/5 |
5)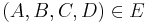
|
(3),(4) |
6)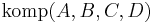
|
(5) |
--Sternchen 20:27, 3. Jun. 2010 (UTC)
Zu Fall 2: (1) ist ein Widerspruch zu (2), denn beides ist o.B.d.A. D.h. es muss für A,B,C und D stimmen und je drei dieser vier Punkte können nicht gleichzeitig kollinear und nichtkollinear sein. --Principella 21:20, 8. Jun. 2010 (UTC)

