Haus der Vierecke aus der Sicht des Heidelberger Winkelkreuzes

Was bisher geschah

--Studentin 01:18, 16. Jul. 2012 (CEST)
--Studentin 18:22, 15. Jul. 2012 (CEST)

Wir betrachten doch sicherlich nur konvexe Vierecke oder??--*osterhase* 16:37, 16. Jul. 2012 (CEST)

Und wie gehts jetzt weiter? Was können wir noch tun, um uns effizient vorzubereiten?
Zieht sich die Thematik "Winlelkreuz" eigentlich durch die ganze Klausur, wie ein roter Faden
oder wird es auch unabhängige Aufgaben geben? Peach22 20:00, 15. Jul. 2012

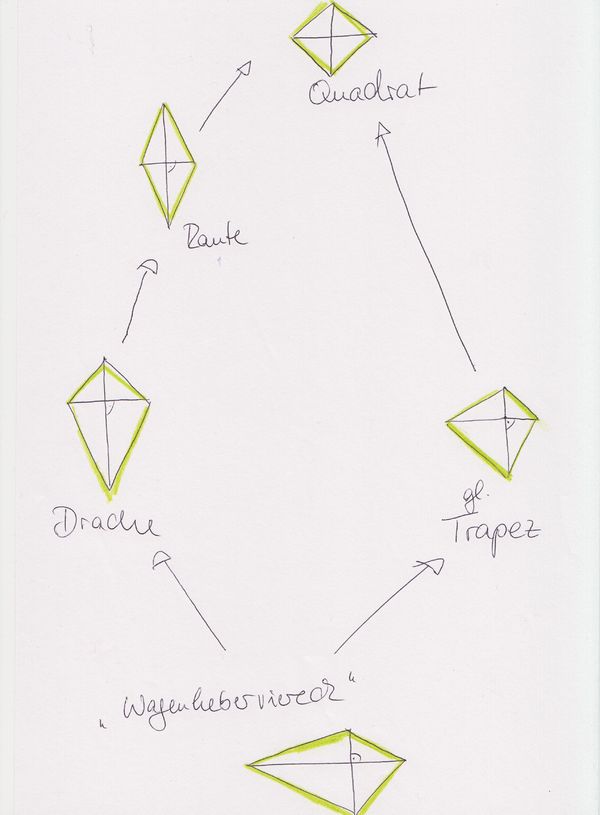
• Quadratkriterium:
  

Ein Rechteck ist genau dann ein Quadrat, wenn seine Diagonalen senkrecht aufeinander stehen.

• weiteres Quadratkriterium:
  

Ein gl. Trapez ist genau dann ein Quadrat, wenn sich seine Diagonalen halbieren und senkrecht aufeinander stehen.

• weiteres Quadratkriterium:
  

Eine Raute ist genau dann ein Quadrat, wenn seine Diagonalen gleich lang sind.

• Rautenkriterium:
  

Ein Drachen ist genau dann eine Raute, wenn sich seine Diagonalen halbieren.

Müsste doch auch gehen!? :D--Tchu Tcha Tcha 22:35, 15. Jul. 2012 (CEST)

Bemerkungen von M.G. zur Einordnung des Winkelkreuzes in die Klausur

• Es wird eine Aufgabe analog zur Aufgabe 3 aus der Klausur des letzten Semesters geben (sowohl ATP als auch AVP):

Die schöne Referendarin Lisa lässt ihre Schüler der 7a (Realschule im Winkelkreuz, Heidelberg-Winkelhausen) mit dem Heidelberger Winkelkreuz bestimmte Vierecke spannen. Aus dieser konstruktiven Begriffserarbeitung erwächst eine Definition des entsprechenden Vierecksbegriffs. Da wir mit absoluter Sicherheit nach den Vierecksspanntätigkeiten nichts anderes wissen, als dass die Diagonalen des Viereckstyps in einer gewissen Relation/in gewissen Relationen zueinander stehen, wird dieses/werden diese als definierende Eigenschaft(en) des Vierecktyps genommen.

• Betrachtung des Hauses der Vierecke bedeutet damit: Klassifizierung der Bewohner des Hauses der Vierecke entsprechend ihrer Diagonaleneigenschaften. (Ein erweitertes Winkelkreuz wird verwendet: Verschiedene Schnittwinkel sind einstellbar.)

--> bedeutet dies, dass das WInkelkreuz in der Mitte drehbar ist? Habe leider nicht das Fach Technik und bin da deshalb nicht sonderlich versiert. Wird das Winkelkreuz, so wie wir es nun kennen und lieben gelernt haben, also so nicht in der Klausur dran kommen sondern verändert?? Bitte um Hilfe!--*osterhase* 11:32, 17. Jul. 2012 (CEST)

@Osterhase: Keine Angst, das Heidelberger Winkelkreuz bleibt in der Klausur starr, also rechtwinklig. Um zu begreifen, was mit dem starren möglich ist, schauen wir auch mal, wie es beschaffen sein müsste, um das zu ermöglichen, was es im rechtwinkligen Zustand nicht gewährleistet. Sie werden die Dinge nur begreifen, wenn Sie über den Tellerand hinaus sehen. Das ist wie in der Schule. Wenn die Schüler begreifen sollen, was ein Quadrat ist, müssen auch Vierecke untersucht werden, die keine Quadrate sind, ins besondere auch solche, die sich nur minimal vom Quadrat unterscheiden, aber eben doch keine Quadrate sind.--*m.g.* 14:40, 17. Jul. 2012 (CEST)

Bin ich fit für die Klausur? Teil 3

Testaufgabe 3.1

Definieren Sie den Begriff gleichschenkliges Trapez mittels des Oberbegriffs Trapez (Viereck mit einem Paar paralleler Seiten) und den Eigenschaften der Diagonalen gleichschenkliger Trapeze.
Lösung Testaufgabe 3.1

Testaufgabe 3.2

Definieren Sie den Begriff gleichschenkliges Trapez nur mittels des Oberbegriffs Viereck und der Diagonaleneigenschaften. Die Eigenschaft, dass zwei Seiten eines gleichschenkligen Trapezes parallel sind, darf nicht benutzt werden.
Lösung Testaufgabe 3.2

Testaufgabe 3.3

Beweisen Sie, dass jedes Viereck entsprechend ihrer Definition aus Teilaufgabe 3.2 ein Paar paralleler Seiten hat.
Lösung Testaufgabe 3.3

Nachdem ich nun meinen Radiergummi zum Schmelzen gebracht habe, stellt sich mir (insbesondere nach der letzten Übung) die Frage, ob die Klausur mit Bleistift geschrieben werden darf und vor allem ANERKANNT wird? Falls die Zeit nicht langt zum Überschreiben mit Kulli, ist die Schreiberei mit dem Bleistift sehr wertvoll ;-)--*osterhase* 17:35, 17. Jul. 2012 (CEST)

@Osterhase Bisher haben wir es immer anerkannt. Ich weis, dass wir uns in juristische Grauzonen begeben. So viel Vertrauen sollten wir aber zueinander haben. --*m.g.* 22:56, 17. Jul. 2012 (CEST) Klasse!--*osterhase* 14:14, 18. Jul. 2012 (CEST)

Noch mehr?

Entwickeln Sie ähnliche Aufgaben wie oben und stellen Sie sich diese gegenseitig.

--*m.g.* 23:22, 16. Jul. 2012 (CEST)