Lösung Aufgabe 11.06 WS 12 13
Inhaltsverzeichnis |
Aufgabe 11.06
Es sei  ein Punkt aus dem Inneren des Winkels
ein Punkt aus dem Inneren des Winkels  . Der Scheitel von
. Der Scheitel von  sei der Punkt
sei der Punkt  . P möge zu den Schenkeln von
. P möge zu den Schenkeln von  jeweils denselben Abstand haben. Beweisen Sie:
jeweils denselben Abstand haben. Beweisen Sie: 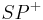 ist die Winkelhalbierende von
ist die Winkelhalbierende von  . Tip: Ssw hilft.
. Tip: Ssw hilft.
Lösung User B......
--B..... 16:55, 24. Jan. 2013 (CET)
Bemerkung --*m.g.* 17:40, 24. Jan. 2013 (CET)
Prinzipiell ist der Beweis korrekt.
Bei dem Nachweis der Dreieckskongruenz nimmt Ssw eine Sonderstellung ein. Während ein Beweisschritt bei der Verwendung von SWS, WSW und SSS 4 Begründungen braucht ( 3 Stücke und der entsprechende Satz bzw. das Axiom) braucht man bei der Verwendung von SsW 5 Begründungen:
3 Stücke, Begründung, dass die drei Stücke so gelegen sind, dass SsW anwendbar ist und natürlich SsW. Konkret heißt das, dass verdeutlicht werden muss, warum wir es mit dem der größeren der beiden Seiten gegenüberliegenden Winkel zu tun haben. Das ist in diesem Fall einfach, da es sich um rechte Winkel handelt.
Feintuning
- Schritt (2):
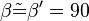 ist in sich nicht konsistent. korrekt: Fehler beim Parsen(Lexikalischer Fehler): |\beta| = |\beta'| = 90\
ist in sich nicht konsistent. korrekt: Fehler beim Parsen(Lexikalischer Fehler): |\beta| = |\beta'| = 90\
- Schritt (3): Die Begründung Definition Abstand ist arg weit hergeholt und trifft es auch nicht ganz. trivial reicht aus. (Jede Strecke ist zu sich selbst kongruent bzw. hat mit sich selbst dieselbe Länge.)
Bei Beweisen, die sich auf Skizzen beziehen, sollten in der Skizze auch alle Objekte auftreten. Fehler beim Parsen(Lexikalischer Fehler): \


