Der Satz des Pythagoras - Eine didaktische Umsetzung
Im Folgenden eine Didaktische Umsetzung, damit der Satz des Pythagoras von den Schülern entdeckt und verstanden werden kann!
Inhaltsverzeichnis |
Wie kann man diesen Satz mit den Schülern erarbeitet?
Mein ehemaliger Mathelehrer in der 7. Klasse hat es auf diese Art und Weise probiert:
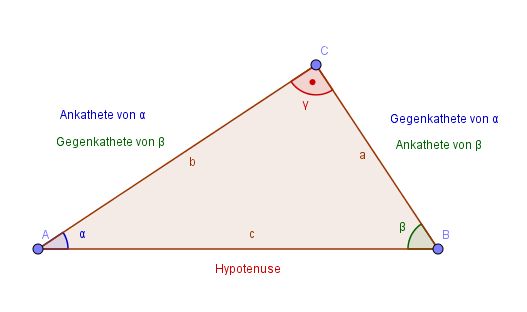
Rechtwinklige Dreiecke dürften euch bekannt sein! Nun kann man nach dem Satz des Pythagoras bei einem rechtwinkligen Dreieck bei welchem zwei bekannte Seiten vorhanden Sind die dritte Seite berechnen. Dies geht ganz einfach mit der Formel a² + b² = c²! Durch entsprechende Umformung lassen sich ebenfalls die Seite a oder b herausfinden. Ein ganz einfacher Satz, denn jetzt jeder von euch anwenden kann:
- Berechne die Hypothenuse: a = 4 cm, b = 2 cm, usw.
Wenn man nun einen Schüler nach Zusammenhängen und Zustandekommen dieses Satzes fragen würde, würde höchst wahrscheinlich keiner eine Antwort geben können.
Warum?
Der Schüler hat keine Gelegenheit bekommen, sich mit dem Satz auseinander zu setzte, ihn zu analysieren, ihn zu verstehen, ihn zu entdecken. Gerade ein Satz wie der Pythagoras erfordert aber genau diese Vorgehensweise. Allerdings wird auch dieser Satz nach obigem Beispiel heute noch nach der Friss – Vogel – oder Stirb – Methode unterrichtet.
Wie könnte man es besser machen?
Der Kathetensatz als Einführung in die Satzgruppe des Pythagoras:
Einstiegsproblem:
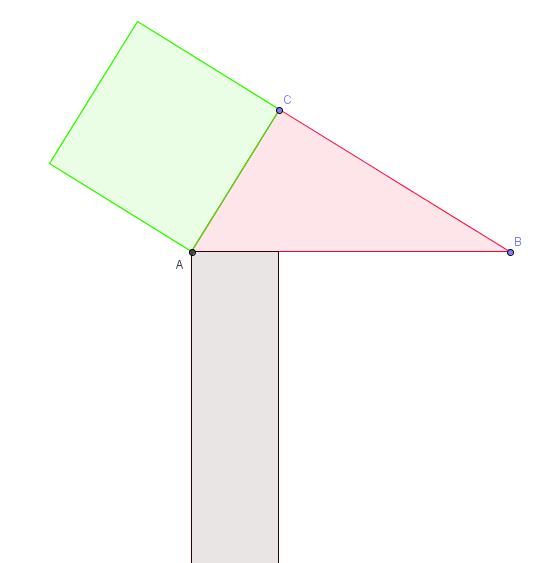
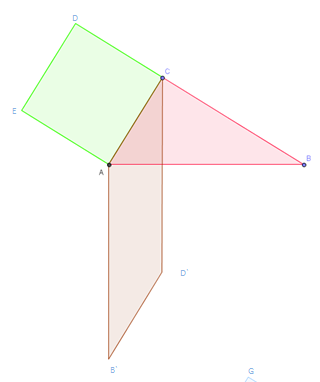
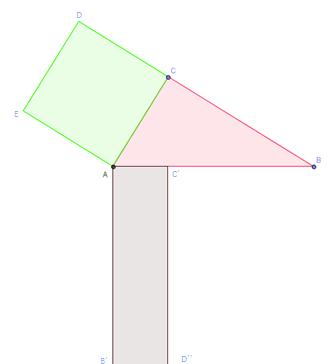
Aus einem Quadrat ein flächengleiches Parallelogramm und aus Parallelogramm ein flächengleiches Rechteck konstruieren.
Aus dem Quadrat über der Kathete b, soll ein flächengleiches Rechteck bei der Hypothenuse errichtet werden:
| Ausgangskonfiguration | Schritt 1 | Schritt 2 | Schritt 3 | Schritt 4 | Schritt 5 |
|---|---|---|---|---|---|
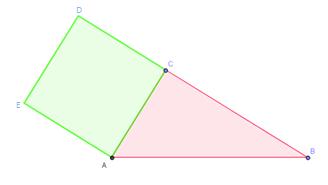 |
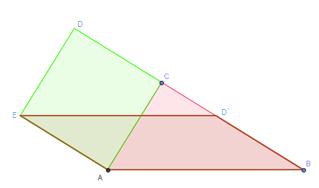 |
 |
 |
|
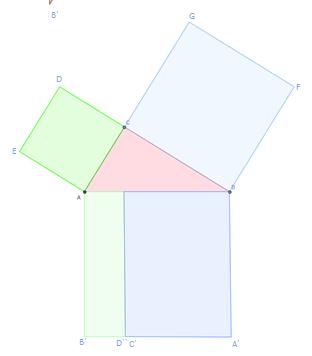
Erstellt man ebenfalls ein flächengleiches Rechteck zum Kathetenquadrat von der Seite a:
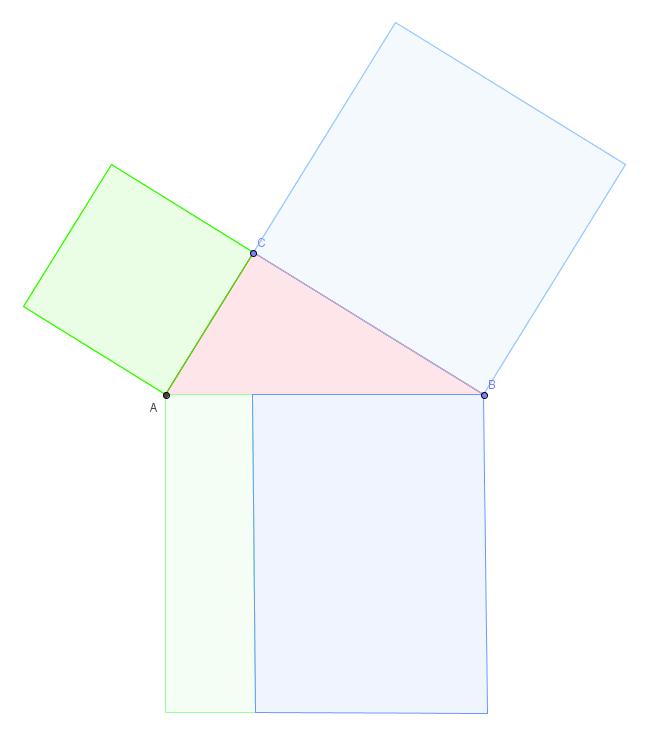
1) Ergebniss a²=c*p
2) Ergebniss b²=c*q
Beweis:
1) EA II BC
2) Dreieck ACDE ist Flächengleich zu dem Parallelogramm ABC’E
2) Parallelogramm um 90° bei A gedreht
3) AB‘ II CC`` Parallelogramm Flächenglich zu Rechteck
das gleiche mit der Seite b
Vermutung = a² + b² = cp + cq = c(p+q) = c²
Starke Deduktive Vorgehensweise: Die Wahrheit des Satzes wird gleichzeitig mit dem Beweis geliefert!
Wo aber war das Einstiegsproblem, das Entdeckende die selbstständige Findung der Zusammenhänge?
Einstiegsproblematik:
Die Seiten a und b können direkt über die Katheten abgelesen werden, die Hypotenuse nicht. Gibt es eine Möglichkeit die Hypotenuse über die Katheten auszurechnen? Stehen sie in einer gemeinsamen Beziehung?
1)Die Reduktiven Methoden zur Satzfindung
Diese Methode ermöglicht, verglichen mit einer reinen deduktiven Herangehensweise wie wir es im obigen Beispiel gesehen haben, eine wirkliche „Findung“ eines Satzes. Womit man einen entscheidenden Lernprozess beim Schüler initiieren kann, der den Schüler darin unterstützt den Satz und seine Zusammenhänge zu verstehen.
1)Induktion
Induktion = das Schließen vom Einzelfall auf die Allgemeinheit
Arbeitsblatt mit verschiedenen rechtwinkligen Dreiecken und einer Tabelle die ausgefüllt werden soll.