Diskussion:Halbebenen oder das Axiom von Pasch
Alte Version
Beweis des Satzes IV.1
Voraussetzung: 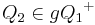
Behauptung: 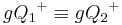 und
und 
| Schritt | Aussage | Begründung |
| (1) | 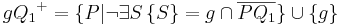 Die Strecke 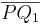 schneidet nicht die Trägergerade g. schneidet nicht die Trägergerade g. |
Definition von Halbebene |
| (2) | 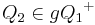 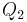 liegt in der Halbebene liegt in der Halbebene 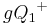 |
Voraussetzung |
| (3) | 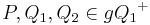 |
Schritt (1) und (2) |
| (4) | Die Strecke 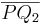 schneidet nicht die Trägergerade g. schneidet nicht die Trägergerade g. |
Schritt (3), Definition von Halbebene |
| (5) | 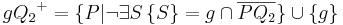 |
Schritt (4) |
| (6) | Es gilt: 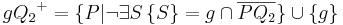 und und
| |
| (7) | 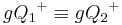 |
Der Definitionsbereich der beiden Halbebene ist identisch - Schritt (6) |
| (8) |  |
Die Mengen 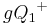 und und 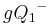 sind disjunkt, gleiches gilt für die Mengen sind disjunkt, gleiches gilt für die Mengen 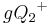 und und 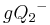 Schritt (7) - Durch Umformung: Schritt (7) - Durch Umformung:
|
Stimmt das so? --Heinzvaneugen 12:23, 23. Jun. 2010 (UTC)
Also, Punkt (4) ist ja eigentlich das, was Sie zeigen wollen, denn wenn die Strecke 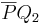 die Trägergerade g nicht schneidet, dann gilt dies ja für jedes beliebige
die Trägergerade g nicht schneidet, dann gilt dies ja für jedes beliebige 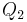 und das heißt, dass Sie statt
und das heißt, dass Sie statt 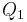 auch
auch 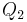 als Repräsentanten ihrer Halbebene nehmen können. Soweit so gut, allerdings können Sie das nicht einfach aus der Definition der Halbebene schließen, weil sie diesen Zusammenhang ja erst noch zeigen müssen (typischer Fall eines Zirkelschlusses). Sie kommen nicht umhin, das Axiom von Pasch an dieser Stelle mit einzubeziehen! Damit wir Pasch verwenden dürfen, müssen wir allerdings voraussetzen, dass P,
als Repräsentanten ihrer Halbebene nehmen können. Soweit so gut, allerdings können Sie das nicht einfach aus der Definition der Halbebene schließen, weil sie diesen Zusammenhang ja erst noch zeigen müssen (typischer Fall eines Zirkelschlusses). Sie kommen nicht umhin, das Axiom von Pasch an dieser Stelle mit einzubeziehen! Damit wir Pasch verwenden dürfen, müssen wir allerdings voraussetzen, dass P, 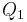 und
und 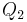 nicht kollinear sind. Der kollineare Fall ist dann nochmal getrennt zu untersuchen, lässt sich dann aber über die Zwischenrelation und über Teilmengenbeziehungen leicht beweisen.--Schnirch 13:59, 23. Jun. 2010 (UTC)
nicht kollinear sind. Der kollineare Fall ist dann nochmal getrennt zu untersuchen, lässt sich dann aber über die Zwischenrelation und über Teilmengenbeziehungen leicht beweisen.--Schnirch 13:59, 23. Jun. 2010 (UTC)
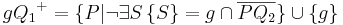 || Voraussetzung und Schritt (5)
|| Voraussetzung und Schritt (5)


 gilt somit auch
gilt somit auch 
