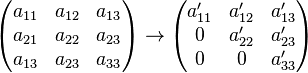Gauß-Algorithmus

Gauß-Algorithmus

Der Gauß-Algorithmus (oder Gauß-Eliminationsverfahren oder "Gauß") ist ein Algorithmus zur Lösung von Linearen Gleichungssystemen (LGS). Das Grundprinzip besteht darin, die Matrix auf Stufen- bzw. Dreiecksform zu bringen, um so die Lösungsmenge leicher 'ablesen' zu können. Im Gauß-Verfahren werden folgende Schritt (Äquivalenzumformungen) verwendet, die die Lösung des LGS nicht verändern.

• Vertauschen von zwei Gleichungen
• Multiplikaiton einer Gleichung mit einer reelen Zahl ($\neq 0$)
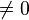• Addition von zwei Gleichung

$\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33} \end{pmatrix} \rightarrow \begin{pmatrix} a'_{11} & a'_{12} & a_{13}'\\ 0 & a'_{22} & a'_{23}\\0 & 0 & a'_{33} \end{pmatrix}$