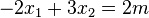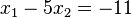Übungen 04
Aus Geometrie-Wiki
Version vom 8. Mai 2013, 10:58 Uhr von Cplicht (Diskussion | Beiträge)
Aufgabe 1
Bestimmen Sie für welche 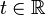 das folgende lineare Gleichungssystem in Matrixdarstellung lösbar ist und geben Sie ggf. die Lösungen an.
das folgende lineare Gleichungssystem in Matrixdarstellung lösbar ist und geben Sie ggf. die Lösungen an.
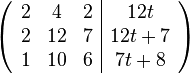
Aufgabe 2
a) Es seien reele Zahlen 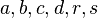 vorgegeben. Begründen Sie, dass das LGS
vorgegeben. Begründen Sie, dass das LGS
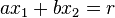
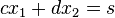
im Falle 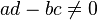 eindeutig lösbar ist und geben Sie die Lösung an.
eindeutig lösbar ist und geben Sie die Lösung an.
b) Bestimmen sie für 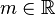 die Lösungsmenge des folgenden LGS:
die Lösungsmenge des folgenden LGS: