Lösung von Aufgabe 3.5 (SoSe 13 P)
Vergleichen Sie die Wahrheitswerte von
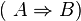 und
und 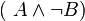 .
.
Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
Ich finde die Aufgabe etwas verwirrend;-/. Habe eine Wahrheitstabelle erstellt, jedoch bin ich mir nicht sicher, ob es stimmt.
Habe in die Wahrheitstabelle: A ,B,A--> B,NICHT B,AundB geschrieben
Als Ergebnis bzw. dass es äquivalent ist muss ja eine Richtung bewiesen werden.
Als Ergebnis habe ich jedoch rausbekommen dass A->B und AundNichtB NICHT ÄQUIVALENT SIND.
Ist es richtig, was ich gemacht habe? Oder soll ich jeweils nur A->B und AundNichtB getrennt betrachten? Sprich zwei Tabellen erstellen da bei der Aufgabenstellung keine Implikation steht sondern UND . HILFE;-/ Was mache ich falsch? --Blumenkind 18:20, 11. Mai 2013 (CEST)Blumenkind
Hallo Blumenkind. Du brauchst nur eine Tabelle machen. Und du liegst richtig damit, dass die Aussagen nicht äquivalent sind.
Wie sieht die Wahrheitstabelle denn aus? Kann Sie jemand füllen? Und anschließend die Bedeutung für den indirekten Beweis mit Widerspruch herleiten?--Tutorin Anne 21:25, 11. Mai 2013 (CEST)
| A | B | 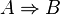 |
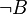 |
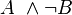
|
|---|---|---|---|---|
| w | w | w | f | f |
| w | f | f | w | w |
| f | w | w | f | w |
| f | f | w | w | w |
Somit haben wir gezeigt, dass sie nicht gleichwertig sind.
Indirekter Beweis mit Widerspruch:
- VSS: Aus A folgt B
- Beh.: AundNichtB Annahme NichtAundB
--> Ich glaube, man kann es nicht beweisen. HILFE;-/ (Blumenkind)
Ich glaube die Tabelle ist falsch. Sieht sie nicht eigentlich so aus?:
| A | B | 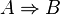 |
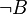 |
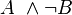
|
|---|---|---|---|---|
| w | w | w | f | f |
| w | f | f | w | w |
| f | w | w | f | f |
| f | f | w | w | f |
Es ist ja AUNDnichtB und nicht AOderNichtB.
Und damit können wir dann in der Tabelle zeigen, das AimpliziertB äquivalent zu nicht(AundNichtB) ist.
Daraus folgt dann, dass das eine die Negation vom anderen ist, und sie nie gleichzeitig stimmen können.
Daraus folgt dann: Wenn die Aussage des Beweises stimmt, muss beim Beweis durch Widerspruch für die Annahme etwas falsches herauskommen. Und wenn die Aussage falsch ist, so wird die Negation stimmen. --Lotta aus der Krachmacherstraße 10:25, 13. Mai 2013 (CEST)
Danke an Blumenkind und Lotta aus der Krachermacherstraße! Lottas Erklärung stimmt so. --Tutorin Anne 10:48, 13. Mai 2013 (CEST)

