Lösung von Aufgabe 8.04 S SoSe 13
Aus Geometrie-Wiki
Version vom 19. Juni 2013, 22:07 Uhr von Illu13 (Diskussion | Beiträge)
z.z.: M1 konvex  M2 konvex
M2 konvex  M1
M1 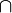 M2 konvex
M2 konvex
Beweis: Wir nehmen an, dass die Punkte A und B im Durchschnitt der beiden Mengen liegt, d.h.:
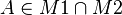 und
und 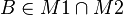
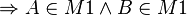 und
und 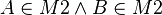
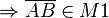 und
und 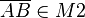 , denn laut unserer Voraussetzung sind M1 und M2 konvex (s. auch Definition IV.4).
, denn laut unserer Voraussetzung sind M1 und M2 konvex (s. auch Definition IV.4).
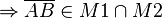
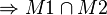 ist konvex (Def.IV.4). q.e.d.
ist konvex (Def.IV.4). q.e.d.
--Illu13 23:07, 19. Jun. 2013 (CEST)

