Der Basiswinkelsatz SoSe 13
Aus Geometrie-Wiki
Version vom 2. Juli 2013, 17:01 Uhr von Tutorin Anne (Diskussion | Beiträge)
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VIII.1 : (gleichschenkliges Dreieck)
Das können sie selbst. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.
Übungsaufgabe
Der Basiswinkelsatz
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
Behauptung: Die Basiswinkel sind kongruent zueinander: |α| = |β| --Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
- Deine Vorausetzung enthält schon Schritt 1. Das ist nicht optimal. Besser ist es, wirklich nur den ersten Teil zu nennen und den 2.Teil wegzulassen. Bei der Behauptung kannst du dir Teil 2 auch sparen, da dieser ja nicht beim Beweis am Ende rauskommt, sondern direkt die Kongruenz da steht. --Tutorin Anne 18:01, 2. Jul. 2013 (CEST)
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 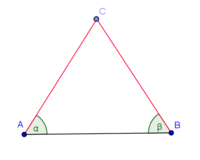
|
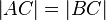
|
Voraussetzung --Nolessonlearned 12:36, 2. Jul. 2013 (CEST) |
| (2) | 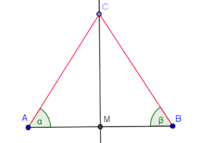
|
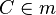 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
(1); Mittelsenkrechtenkriterium --Nolessonlearned 12:37, 2. Jul. 2013 (CEST) |
| (3) | |
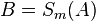
|
Streckentreue bzw Abstanderhaltung der Geradenspiegelung --Nolessonlearned 12:48, 2. Jul. 2013 (CEST) |
| (4) | |
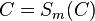
|
C∈m mit m:= Spiegelachse ⇒ C ist Fixpunkt--Nolessonlearned 12:51, 2. Jul. 2013 (CEST) |
| (5) | |
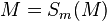
|
M∈m mit m:= Spiegelachse ⇒ M ist Fixpunkt--Nolessonlearned 12:53, 2. Jul. 2013 (CEST) |
| (6a) | |
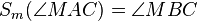
|
Winkeltreue der Geradenspiegelung--Nolessonlearned 12:57, 2. Jul. 2013 (CEST) |
| (6b) | |
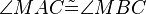
|
... |
Guter Beitrag, Nolessonlearnd! Einige Begründungen sind noch zu ergänzen:
- Jeder Schritt sollte irgendwo auftauchen, damit er auch ein Recht hat, nicht weggelassen werden zu können. Ergänzt die Nummern!
- Begründung zu Schritt 1 sollte noch ergänzt werden
- Begründung Schritt 6 ist komplexer. Damit das klarer ist, habe ich deshalb noch ein Zwischenschritt eingefügt. Die Begründungen müssen noch ergänzt werden.--Tutorin Anne 18:01, 2. Jul. 2013 (CEST)

