Der Zusammenhang von Seitenlängen und Winkelgrößen im Dreieck SoSe 13
Aus Geometrie-Wiki
Version vom 4. Juli 2013, 22:13 Uhr von *m.g.* (Diskussion | Beiträge)
--*m.g.* 19:35, 3. Feb. 2013 (CET)
(IV) mit Definition Zwischen zu begründen, passt nicht. Sie müssten begründen, warum die Forderungen der Definition erfüllt sind. (I) ist schon mal gut, reicht aber nicht ganz. Tipp: Voraussetzungen
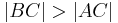 und Schritt (I).
und Schritt (I).--Natürliches Mineralwasser 11:42, 4. Feb. 2013 (CET)
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 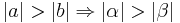
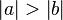
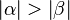
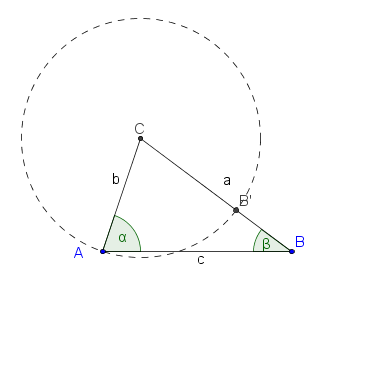
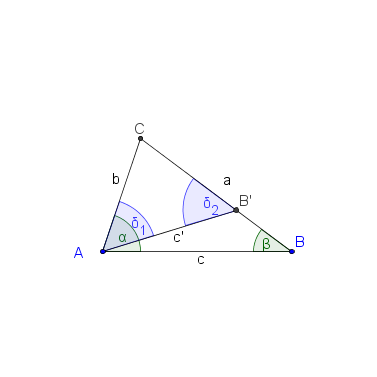
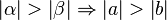
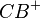 existiert ein Punkt
existiert ein Punkt 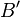 , der zu
, der zu  den Abstand der Länge
den Abstand der Länge 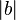 der Strecke b hat.
der Strecke b hat. 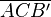 ist gleichschenklig, wobei
ist gleichschenklig, wobei  und
und 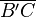 die zueinender kongruenten Seiten sind.
die zueinender kongruenten Seiten sind.