Lösung von Zusatzaufgabe 9.1P (SoSe 13)
Aus Geometrie-Wiki
Version vom 11. Juli 2013, 21:30 Uhr von Regenschirm (Diskussion | Beiträge)
- Was versteht man unter der Parallelentreue einer Geradenspiegelung?
- Beweisen Sie die Parallelentreue einer Geradenspiegelung.
Tipp: Im Wiki nachlesen und den Beweis dann indirekt führen.--Tutorin Anne 18:21, 26. Jun. 2013 (CEST)
- Zwei Geraden sind parallentreu, wenn bei der Geradenspiegelung zueinander parallelen Geraden p1 und p2 ebensfalls zueinader parallel abgebilder werden. Kurz formuliert:
--> p1 II p2 --> p1` II p2 ` wobei Sg (P1)= P1` und Sg(P2)=P2`
- Beweisdurchführung
- Vor.: p1 II p2, Sg (P1)= P1` und Sg(P2)=P2`
- Beh.: p1`II p2`
1. Sg (p1)= p1` und Sg(p2`) Voraussetzung
2. p1 II p2 Voraussetzung
3.
--> HILFE!!!! ICH KOMM NICHT MEHR WEITER. IRGENDWIE BIN ICH DURCHEINANDER GEKOMMEN. WAS MACHE ICH FALSCH?--Blumenkind 18:51, 4. Jul. 2013 (CEST)BLUMENKIND 18:50, 4.Juli
Probier es mal, wie Anne schon oben angemerkt hat, über einen indirekten Beweis. Wie muss also die Annahme lauten?--TobiWan 12:28, 5. Jul. 2013 (CEST)
- Voraussetzung und Behauptung sind richtig.
- Das ist leider kein Beweis, da nur, weil Geraden auf Geraden abgebildet werden, diese nicht unbedingt parallel sind.
- Tipp: Gehe indirekt vor, indem du annimmst dass P1 und p2 einen Schnittpunkt haben.--Tutorin Anne 14:22, 8. Jul. 2013 (CEST)
| Voraussetzung | 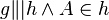
|
| Behauptung | 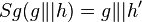
|
| Annahme | 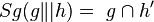
|
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | 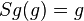 |
Voraussetzung, Def. Geradenspiegelung |
| 2 | 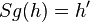 |
Voraussetzung, Def. Geradenspiegelung |
| 3 | 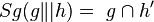 |
Annahme |
| 4 | 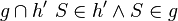 |
1) 2) 3) |
| 5 | 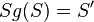 |
4) Def. Geradenspiegelung |
| 6 | 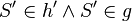 |
2) 5) |
| 7 | 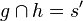 |
6) |
| 8 | Widerspruch, Annahme ist zu verwerfen, Behauptung stimmt | 7) |
--Regenschirm 22:30, 11. Jul. 2013 (CEST)

