Lösung von Aufgabe 11.2P (SoSe 13)
Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.
Umkehrsatz: Wenn Wechselwinkel an g und h kongruent sind, dann sind g und h parallel zueinander.
Vor.: 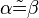
Beh.: gIIh
Anmerkung: Ich habe mir eine Skizze gezeichnet: 2 Geraden a und b, die von einer dritten Geraden geschnitten wird mit a geschnitten c = H und b geschnitten c= G, sowie Punkt A` ist Element a
und A ist Element b (gehört alles zur Voraussetzung)
Beweis:
1) Punkt S ist Mittelpunkt von der Strecke GH Def. Mittelpunkt
mit IGSI = ISHI
2)  = <AGS und
= <AGS und  = <SHA` (1), VORAUSSETZUNG
= <SHA` (1), VORAUSSETZUNG
3) D (S,180) <AGS = <SHA` Def. Punktspiegelung
4) GH+ II HA` Eigenschaft Punktspiegelung, (3), Winkelmaßerhaltung, Winkeltreue
5) aIIb 4
--Blumenkind 10:50, 12. Jul. 2013 (CEST)Blumenkind 10:49, 12. Juli

